功-能定理的推导

---

简介

功-能定理指出，外力对物体所做的净功等于该物体动能的变化率。功-能定理指的是所有作用在物体上的力的功，而不是单个力的功。根据功-能定理，动能被定义为将物体从静止状态加速到所需速度所需的功。

什么是功-能定理？

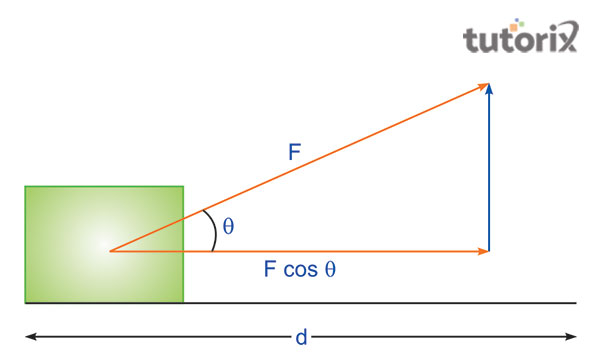
图 1：功-能定理示意图

功-能定理的公式表示为 W= FdcosӨ，其中 W 表示功，F 表示作用在物体上导致其从初始位置发生位移的外力，d 表示物体两个不同位置之间的距离。物体由于所具有的能量而产生的运动称为动能。

功-能定理的推导

根据运动学公式，功-能定理的推导可以定义为 v² = u² + 2as，其中 V 表示物体的最终速度，u 表示物体的初始速度，a 表示恒定加速度，s 表示物体的位移。

根据牛顿第二定律 F = ma，因此该公式也可以写成 1/2 mv² - 1/2 mu² = F.d

这里，W 等于 F.d，而 K.E. 等于 (mv²)/2，则公式可以表示为 K_f – K_i = W。

因此，ΔK = W，其中 ΔK 表示 Kf – Ki，即动能的变化。

所以，可以说对特定物体所做的功等于其动能的变化。

变力下的功-能定理

日常生活中常见的外部力被称为变力。从功-能定理的推导角度来看，变力的公式较为复杂。

它可以表示为 $\Delta W = F\left ( x \right ) \Delta x$，其中功的变化依赖于所施加的外力和 x 的变化。

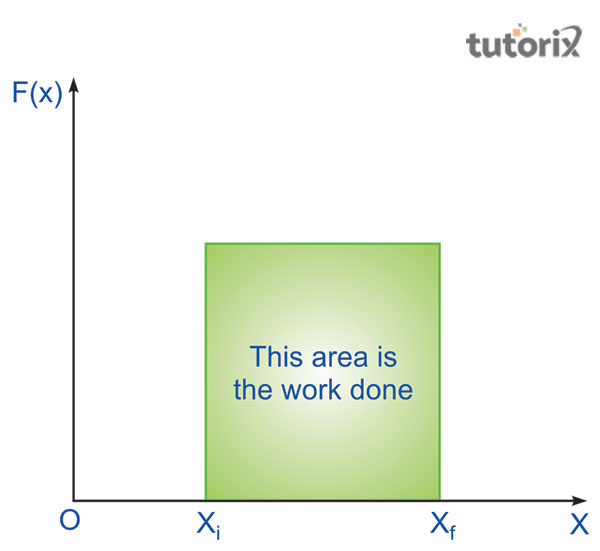
图 2：变力下的功-能定理

随着动力的变化，公式描述为 dK/dt = d/dt(1/2 mv²)，根据牛顿第二定律，加速度变为 dK/dt = mav。

由于 F = ma，则速度随时间的变化率也随之改变，因此公式变为 dK/dt = F.dx/dt，如果从等式两边推导出时间，则公式表示为 dK = Fdx 或 ΔK = W。

由于该公式证明了功-能定理依赖于变力。

恒力下的功-能定理推导

根据牛顿第二定律，F = ma，其中 m 表示在恒力 F 的作用下运动的物体的质量，a 表示物体的加速度。

对于恒力推导，公式为 Fd = 1/2 m.v₂² – 1/2 m v₁²，其中 F 表示恒力，mv 表示物体的质量速度。在公式中，d 表示物体初始位置和最终位置之间的距离，这里公式表示 K₂ = m.v₁²/2，表示特定物体的最终动能。

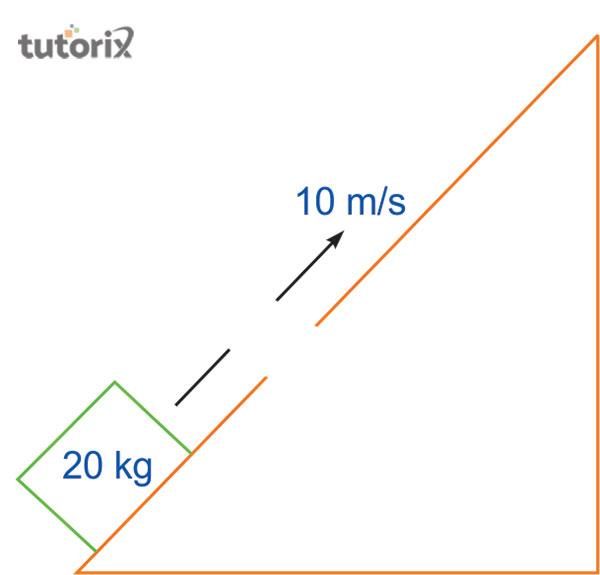
图 3：恒力下的功-能定理推导

物体的量为 K₁=mv₁²/2，它是特定物体的初始动能。

然后公式变为 W = K₂-K₁=ΔK，其中 ΔK 表示该特定物体的动能变化。

从这个特定的公式可以看出，力对特定物体所做的功等于该物体动能的变化。

功-能定理的特征及其应用

• 当物体以恒定速度运动时，动能不变，合外力所做的功等于零。

• 功完成后能量才会表现出来，因此能量可以通过物体被其他粒子带走而减少。

• 它对于理解多个力作用下刚体的运动情况非常有用。

功-能定理的有趣事实

• 它指出外力对物体所做的功等于该特定物体的动能。

• 牛顿第二定律在功-能定理中非常适用。

• 对物体所做的功可以是正的也可以是负的。

结论

功是指外力对物体施加的力，使其从初始位置发生位移。它等于力在位移方向上的分量与位移大小的乘积。功可以用焦耳来衡量，它是它的 SI 单位。所做的功表示从单个物体转移的总能量，施加外力会影响物体的位移方向。

常见问题

问 1：功-能定理证明了什么？

答：功-能定理阐明了物体动能与对物体所做的功之间的关系。当对物体施加动能导致物体发生位移时，我们就说做了功。

问 2：功-能定理不适用于所有类型的力的原因是什么？

答：并非所有类型的力都包含非保守因素，因此功-能定理不适用于所有类型的力。功-能定理的公式为 W = KE_f - KE_i = 1/2mv_f² - 1/2mv_i²。

问 3：为什么功有时是负的？

答：当施加的力与位移方向相反时，功为负。如果力与位移方向相同，则功为正。

问 4：功-能定理的意义是什么？

答：功-能定理对于测量物体的动能非常有用。它也适用于测量力。