无权图的应用、优点和缺点

---

图是如何工作的？

一组相互连接的事物被称为图。它们可以代表任何事物，从纯粹的数学概念到现实生活中的物体、事件和现象。例如，一个图可以表示一个具有家族关系的个人列表。类似地，一个城市网络通过道路连接在一起。

通常，我们将网络的元素描述为节点或顶点，而它们之间的连接被称为边或弧。

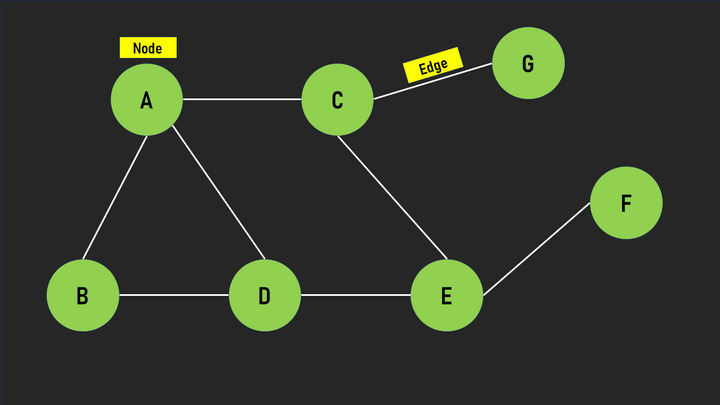
图1 - 带有节点和边的图的可视化表示

无权图：它是什么？

如果没有任何边附加成本或权重，则该图被称为无权图。它们只显示两个顶点之间存在关系。

简单来说，当我们关注两个节点是否连接或断开连接时，我们将网络称为无权图。我们将具有边连接的节点称为彼此相邻或邻接。

图2 - 无权图

在这篇文章中，我们将探讨无权图的简单性，其中顶点之间的关系以不包含边权重的复杂性的方式显示。无权图在许多不同领域都有许多应用，包括网站和社交网络。了解这种类型的图的优点和缺点及其在解决问题中的应用。

无权图：优点

• 由于无权图考虑了任何两个节点之间是否存在连接，因此这些概念易于阅读和理解。

• 无权图比有权图消耗更少的存储空间，因为它们只需要少量内存来存储有关边是否存在的数据。

• 无权图易于理解，因为它们描述了连接的存在，并且不需要分析边权重。

• 可以使用无权图实现树形数据结构。

• 包括 DFS 和 BFS 在内的几种算法都使用无权图。

• 有助于最佳地可视化具有连接但大小不可比的问题。

• 由于不需要存储或处理边权重，因此无权图比有权图更容易处理。

• 无权图适用于边权重无关紧要或未知的问题。

• 当边权重不重要或不明确时，无权图是最佳选择。

• 无权图比有权图更易于管理，因为它们不需要存储或操作边权重。

无权图：缺点

• 无权图无法描述某些关系，包括图中两个节点之间的成本或距离。

• 在无权图的情况下，没有边权重。因此，对于需要了解节点之间距离或评估最短路径的目的而言，它没有帮助。

• 由于它们无法提供有关节点之间连接的值或强度的详细信息，因此无权图可能比有权图的信息量少得多。

无权图：应用

• 使用无权图显示在大小方面彼此之间没有关系的统计数据。

• 无权图表示计算过程的流程。

• 可以使用节点和边来表示图像分割，其中节点表示像素，边表示邻接连接。

• 人工智能可以使用状态空间表示来解决问题和做出决策。

• 例如，工作场所中的数据网络表示，例如万维网。

无权图在实时中的使用

• 可以使用无权图解决难题。

• 此功能可用于确定两个人在社交网络平台上是否相互关联。

• 它用于具有各种实际应用的哈密顿图，包括基因组映射，以组合多个小的遗传信息片段。

• 可以使用此方法表示电路的示意图。

• 无权图用于描述游戏场景中每个可能的移动。

• 因为它以无权图的形式表示社交网络中人与人之间的联系，所以它被用于社交媒体平台。

邻接矩阵

邻接矩阵是表示无权图的一种有效方法。该矩阵是一个“n”乘“n”的 1 和 0 数组，其中“n”是节点的总数。如果与元素 $\mathrm{a_{ij}}$ 关联的值为 1，则存在连接第 i 个节点和第 j 个节点的边。如果 $\mathrm{a_{ij} \: = \: 0}$，则确实没有边连接这两个节点。

图3 - 邻接矩阵示例

两个基本假设决定了矩阵表示

• 通过将节点映射到整数，可以为每个节点分配不同的整数编号。在上述情况下，映射为 A 到 1，B 到 2，C 到 3，D 到 4，E 到 5。

• 考虑到可用内存有足够的空间来容纳它，可以使用节点总数为 n×n 矩阵分配连续的内存。

注意 - 如果这些假设不准确或图看起来很稀疏，则使用邻接表。

邻接表

图4 - 邻接表示例

您在一个链表中跟踪每个节点的邻居。这种方法的主要优点是存储图数据的内存量不需要是连续的。但是，我们确实失去了矩阵表示的“O(1)”访问复杂性，这是一个宝贵的特性。

无论 i 和 j 的实际值如何，我们都可以以一致的时间量查询“aij”并获取有关第 i 个节点和第 j 个节点邻接的数据。我们可以使用链表遍历整个列表。在最坏的情况下，除搜索查询中的第 j 个顶点以外的所有顶点都是第 i 个节点的邻居。因此，为了确定两个节点是否没有连接，我们将检查链表中找到的 [n - 2 ∈ O(n)] 个项目。

结论

本文讨论了无权图的表示。当我们只需要了解两个事物是否通过边直接连接时，这种类型的图很有效。