Javascript 中的 AVL 树旋转

为了保持平衡，AVL 树可能会执行以下四种旋转：

• 左旋转
• 右旋转
• 左-右旋转
• 右-左旋转

前两种旋转是单旋转，后两种旋转是双旋转。要使树失去平衡，我们至少需要一棵高度为 2 的树。通过这棵简单的树，让我们逐一了解它们。

左旋转

如果在右子树的右子树中插入一个节点时树变得不平衡，那么我们执行一次左旋转：

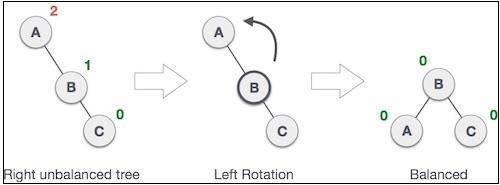
在我们的示例中，节点 **A** 由于在 A 的右子树中插入了一个节点而变得不平衡。我们通过将 **A** 设为 **B** 的左子树来执行左旋转。此旋转也称为 LL 旋转。让我们看看如何实现它：

function rotationLL(node) {
let tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}

右旋转

如果在左子树的左子树中插入一个节点，AVL 树可能会变得不平衡。然后树需要右旋转。

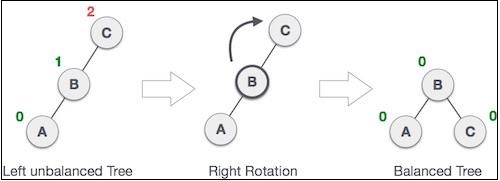
如图所示，通过执行右旋转，不平衡的节点成为其左子节点的右子节点。这也被称为 RR 旋转。让我们看看它在代码中的样子：

function rotationRR(node) {
let tmp = node.right;
node.right = tmp.left;
tmp.left = node;
return tmp;
}

左-右旋转

双旋转是已经解释过的旋转版本的稍微复杂一些的版本。为了更好地理解它们，我们应该注意旋转时执行的每个动作。让我们首先检查如何执行左-右旋转。左-右旋转是左旋转后接右旋转的组合。

状态	动作
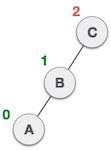
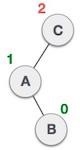	在左子树的右子树中插入了一个节点。这使得 **C** 成为一个不平衡的节点。这些情况会导致 AVL 树执行左-右旋转。
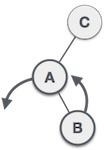	我们首先对 **C** 的左子树执行左旋转。这使得 **A** 成为 **B** 的左子树。
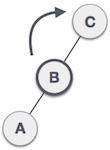
	节点 **C** 仍然不平衡，但是现在，这是因为左子树的左子树。
	我们现在将对树进行右旋转，使 **B** 成为此子树的新根节点。**C** 现在成为其自身左子树的右子树。
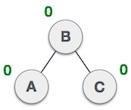	树现在已经平衡。

这也被称为 LR 旋转，因为我们首先执行左旋转，然后执行右旋转。可以使用前面两种方法实现如下：

function rotationLR(node) {
node.left = rotationRR(node.left);
return rotationLL(node);
}

右-左旋转

第二种类型的双旋转是右-左旋转。它是右旋转后接左旋转的组合。

状态	动作
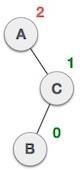	在右子树的左子树中插入了一个节点。这使得 **A** 成为一个不平衡的节点，平衡因子为 2。
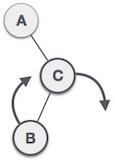	首先，我们在 **C** 节点执行右旋转，使 **C** 成为其自身左子树 **B** 的右子树。现在，**B** 成为 **A** 的右子树。
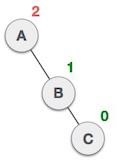	节点 **A** 仍然不平衡，因为其右子树的右子树需要左旋转。
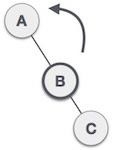	通过使 **B** 成为子树的新根节点来执行左旋转。**A** 成为其右子树 **B** 的左子树。
	树现在已经平衡。

这也被称为 RL 旋转，因为我们首先执行右旋转，然后执行左旋转。可以使用前面两种方法实现如下：

function rotationRL(node) {
node.right = rotationLL(node.right);
return rotationRR(node);
}

Sai Subramanyam

更新于: 2020-06-15

274 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习