方位角量子数 - 定义、辅助内容和常见问题

---

引言

方位角量子数及其研究对于理解物质的量子特性至关重要。原子是物质的基本单元。根据玻尔原子模型，原子包含一个小的中心核心，称为原子核，充满正电荷。电子围绕原子核在特定圆圈（称为轨道）中旋转。圆周路径由电子和原子核之间静电力产生的向心力维持。不同的轨道具有不同的能量。由于它无法解释海森堡不确定性原理和粒子的波粒二象性，因此形成了一个新的分支，称为量子力学。它是由埃尔温·薛定谔发展起来的。他根据像电子这样的粒子的波动性发展了这一点。量子力学的主要概念是能量的量子化、粒子的波粒二象性和不确定性原理。

什么是量子数？

量子数用于确定电子的位置。它描述了原子的能级。不同的轨道具有不同的尺寸、形状和方向。量子数代表原子的轨道的不同特性。这意味着量子数提供了关于电子大小、形状、位置和空间方向的完整信息。有四个量子数来解释电子的状态。它们是

• 主量子数 (n)。

• 磁量子数 (ml)。

• 方位角量子数 (l)。

• 自旋量子数 (ms)。

什么是主量子数？

这个数字提供了关于电子能级轨道的信息。主量子数表示电子离原子核的距离。它用符号 n 表示。它取从 1 到无限大的正整数（即）n=1,2,3……

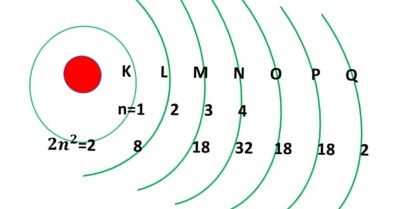
根据 n 的值，电子层分别用K、L、M、N、O等表示。

每个轨道的电子占据数由$\mathrm{2n^2}$定义。

如果 n=1，则 K 轨道有两个电子。

如果 n=2，则 L 轨道有 8 个电子，依此类推。

如果电子从较低的能级跃迁到较高的能级，则 n 值增加，这称为吸收。如果电子从较高能级跃迁到较低能级，则 n 值减小，这称为发射。在吸收过程中，电子吸收能量；在发射过程中，电子释放能量。

主量子数还给出了一个方程，用于计算氢原子的能量，如下所示：

$$\mathrm{En =-\frac{2\pi^2 me^4 Z^2}{n^2 h^2}}$$

从 K 到 Q，轨道的能量值逐渐增加。

定义：方位角量子数

这个数字通过确定轨道的轨道角动量来提供关于轨道构型的信息。在多电子原子中，电子的能量路径不同，因此它们的角动量也不同（即）多电子原子中存在亚层。这个数字用l表示。方位角量子数由主量子数决定。它提供了关于亚层的形状、能量和角动量的详细信息。方位角量子数l的值为 0 到 (n-1)。

它们用s、p、d、f……表示。

让我们取 n=1，它是 K 层。

方位角值为 l=0。它只有一个亚层。它是 1s。

如果 n=2，它是 L 层。

方位角值为 l=0,1。它有两个亚层。它们是 2s、2p。

如果 n=3，它是 M 层。

方位角值为 l=0,1,2。它有三个亚层。它们是 3s、3p、3d。

主量子数(n)	电子层	方位角量子数(l)	亚层数	亚层
1	K	0	1	1s
2	L	0,1	2	2s, 2p
3	M	0,1,2	3	3s, 3p, 3d
4	N	0,1,2,3	4	4s, 4p, 4d, 4f

表 1：主量子数和方位角量子数的填充

因此，亚层数和主量子数相同。

方位角量子数的历史

玻尔利用量子化的概念并提出了他的理论。根据他的理论，电子绕原子核旋转而不损失能量。当电子从较低的能级跃迁到较高的能级时，它会获得能量；当电子从较高的能级跃迁到较低的能级时，它会损失能量。他用量子数 n=1,2,3……表示能级，如 K、L、M 等。但这无法解释原子的电场和磁场效应，而且他的概念只适用于较小的原子。它也无法解释电子的附加行为。除了主量子数之外，还增加了三个量子数来描述多电子原子的行为。

方位角量子数是从玻尔原子模型中沿用过来的。最低能级具有零角动量。也就是说，它被认为是一维的。在三维空间中，它像摆一样在圆形路径上振荡。

结论

原子由中心处的原子核组成，周围环绕着电子。量子数用于数值确定电子的位置。所有四个量子数都提供了关于电子的形状、大小和方向的信息。这里讨论了主量子数和方位角量子数。

常见问题

Q1. 什么是泡利不相容原理？

答：泡利不相容原理是量子力学的理论。根据该理论，没有两个费米子可以处于相同的态。对于电子而言，两个电子不能处于相同的量子态。

如果粒子服从这个原理，则被称为费米子。例如：电子、原子、中子。

如果粒子不服从这个原理，则被称为玻色子。例如：光子。

Q2. 说明洪特规则。

答：该规则解释了电子在轨道中的分布。它指出，首先，轨道的每个亚轨道都被单个电子占据。之后，才会发生电子的配对。

Q3. 量子数的重要性是什么？

答：量子数描述了电子在空间中的位置。根据四个量子数的薛定谔波动方程，提供了关于电子特性的完整信息。根据泡利不相容原理，两个电子不能处于四个量子能级。这些量子数描述了原子的能级、亚层和电子的方向。自旋量子数表示电子的自旋方向。

Q4. 什么是海森堡不确定性原理？

答：海森堡不确定性原理描述了不可能同时找到电子的位置和动量。

Q5. 什么是原子轨道？

答：表示电子位置及其波动性的数学量被称为原子轨道。