角动量 - 定义、公式、单位、常见问题

---

引言：什么是动量？

角动量和线性动量都是矢量。既具有大小又具有方向的物理量称为矢量。例如：位移、速度、动量等。动量是粒子速度和质量的乘积。在线性运动中，它被称为线性动量，表示为P。

$$\mathrm{线性动量 = 质量 \times 速度}$$

角动量

如果一个粒子沿圆形路径运动，则称其处于圆周运动。粒子在圆周运动中的动量称为角动量。对于封闭路径，粒子的总角动量是恒定的。角动量定义为圆形路径的半径和线性动量的乘积。其单位为$\mathrm{Kg\:m^2 s^{−1}}$。角动量的量纲公式为$\mathrm{[M\:L^2\:T^{−1}]}$。

$$\mathrm{\overrightarrow{L} =\overrightarrow{r}\:\times\: \overrightarrow{P}}$$

或

$$\mathrm{\overrightarrow{L}= \overrightarrow{I}\:\times\:\overrightarrow{\omega}}$$

这里，

r - 半径

p - 线性动量

I - 惯性矩

ω - 角速度

粒子的速度是距离 (S) 变化率。类似地，角速度是粒子每秒 (t) 的角位移 (θ)。线速度和角速度的关系为

$$\mathrm{v=rω}$$

角动量公式

让我们考虑一个刚体，它有 n 个粒子绕垂直于它的轴旋转。每个粒子的质量为$\mathrm{m_1 ,m_2,m_3...................m_n}$，它们到旋转轴的距离为$\mathrm{\overrightarrow{r_1},\overrightarrow{r_2},\overrightarrow{r_3}.................\overrightarrow{r_n}}$。由于粒子位置不变，因此它们以相同的角速度 ω 旋转。

粒子 1 在旋转运动中的速度为$\mathrm{v_1=r_1\:ω}$

类似地，粒子 2、3、4......................................n 为

$\mathrm{v_2 = r_2 ω,\:v_3 = r_3 ω , …………. v_n = r_n\:ω}$。

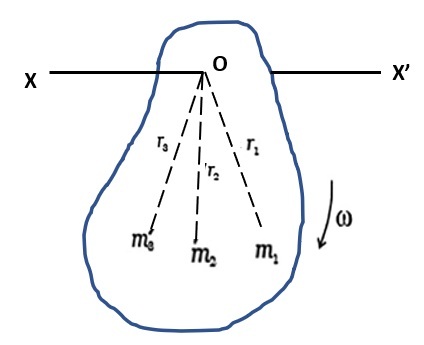
粒子 1 的线性动量为$\mathrm{p_1 = m_1 v_1}$

类似地，粒子 2、3........................n 的线性动量为$\mathrm{p_2 = m_2 v_2,\:p_3 = m_3 v_3,\:and\:so\:on\:p_n = m_n v_n.}$

第一个粒子的角动量为$\mathrm{L_1=r_1\:p_1}$

类似地，粒子 2、3..............n 的角动量为$\mathrm{L_2 = r_2 p_2, \:L_3 = r_3 p_3, ……… L_n = r_n p_n}$。

代入$\mathrm{p_1,p_2,p_3..........................p_n}$的值。

$$\mathrm{L_1=r_1 m_1 v_1}$$

$$\mathrm{L_2=r_2 m_2 v_2}$$

$$\mathrm{L_3=r_3 m_3 v_3}$$

$$\mathrm{L_n=r_n m_n v_n}$$

物体的总角动量为

$$\mathrm{L=r_1 m_1 v_1+r_2 m_2 v_2+r_3 m_3 v_3+...................r_n m_n v_n}$$

现在代入$\mathrm{v_1,v_2,v_3.......................v_n}$的值

$$\mathrm{L=m_1 r_1^2 \omega+m_2 r_2^2 \omega+m_3 r_3^2 \omega+.................+m_n r_n^2 \omega}$$

$$\mathrm{L=(m_1 r_1^2+m_2 r_2^2+m_3 r_3^2+................................m_n r_n^2)\omega}$$

$$\mathrm{L = I \omega}$$

$$\mathrm{I=m_1 r_1^2+m_2 r_2^2+m_3 r_3^2+...........................+m_n r_m^2}$$

这是物体绕其旋转轴的惯性矩的所需方程。

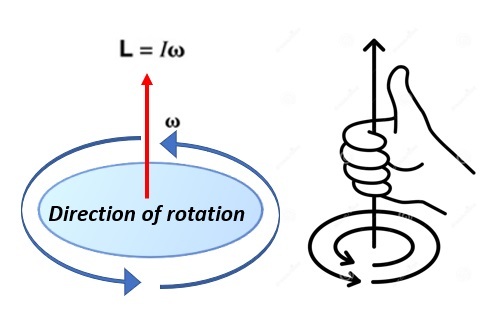
右手螺旋定则

右手定则给出角动量的方向。如果除了拇指以外的四个手指弯曲并显示物体的旋转方向，则向上指的拇指表示角动量、角速度和扭矩的方向。

角动量和扭矩

角动量定义为线性动量的矩。扭矩是使物体绕轴旋转的力。扭矩也是矢量。扭矩的单位为 Nm。

$$\mathrm{\overrightarrow{\tau}=\overrightarrow{r}\times \overrightarrow{F}=rFsin\theta}$$

对于旋转体，

$$\mathrm{\overrightarrow{\tau}=\overrightarrow{I}\times \overrightarrow{\alpha}}$$

这里

$\mathrm{\overrightarrow{\tau}}$= 扭矩

$\mathrm{\overrightarrow{I}}$= 惯性矩 I

$\mathrm{\overrightarrow{\alpha}}$= 角加速度

刚体的扭矩

假设一个刚体包含 n 个粒子，这些粒子绕通过它的轴旋转，角动量为 ω。每个粒子的质量为$\mathrm{m_1, m_2,....... m_n}$，它们到旋转轴的距离为$\mathrm{r_1,r_2..................r_n}$。由于它是刚体，因此粒子的角动量与 ω 相同，但粒子的线速度不同，为$\mathrm{v_1,v_2..........................v_n}$。

粒子 1 的角加速度为

$$\mathrm{a_1=\frac{dv_1}{dt}=\frac{d(r_1 ω)}{dt}\:\:\:\:\:(\frac{dr}{dt}=v=rω)}$$

$$\mathrm{a_1=r_1\frac{dω_1}{dt}= r_1\:\alpha\:\:\:\:\:(\frac{dω}{dt}=\alpha)}$$

类似地，粒子 2,.... n 为

$$\mathrm{a_2 = r_2\:\alpha}$$

$$\mathrm{a_n = r_n\:\alpha}$$

作用在粒子 1 上的力为

$$\mathrm{\overrightarrow{F_1}=m_1\overrightarrow{a_1}=m_1\overrightarrow{r_1}\alpha}$$

粒子 2,.... n 上的力为

$$\mathrm{\overrightarrow{F_2}=m_2\overrightarrow{r_2}\overrightarrow{\alpha}..............\overrightarrow{F_n}=m_n\overrightarrow{r_n}\overrightarrow{\alpha}}$$

粒子 1 的扭矩为

$$\mathrm{\overrightarrow{\tau_1}=\overrightarrow{r_1}\times \overrightarrow{F_1}=\overrightarrow{r_1}\times m_1\overrightarrow{r_1}\overrightarrow{\alpha}}$$

$$\mathrm{\overrightarrow{\tau_1}=m_1r_1^2\alpha}$$

类似地，粒子 2,....n 为

$$\mathrm{\overrightarrow{\tau_1}=m_2 r_2^2 \alpha}$$

$$\mathrm{\overrightarrow{\tau_n}=m_n r_n^2 \alpha}$$

刚体的总扭矩为

$$\mathrm{\overrightarrow{\tau}=m_1 r_1^2 \alpha+ m_2 r_2^2 \alpha+.......................+m_n r_n^2 \alpha. }$$

$$\mathrm{\overrightarrow{\tau}=(m_1 r_1^2+m_2 r_2^2+.......................+m_n r_n^2)\alpha}$$

$$\mathrm{\overrightarrow{\tau}=I\alpha}$$

$$\mathrm{扭矩 = 惯性矩 \times 角加速度}$$

角动量和扭矩之间的关系

刚性旋转体的扭矩为，

$$\mathrm{\overrightarrow{\tau}=\overrightarrow{I}\times \overrightarrow{\alpha}}$$

$$\mathrm{\overrightarrow{\tau}=\overrightarrow{I}\times \frac{d\overrightarrow{\omega}}{dt}\:\:\:\:\:\:\:(\alpha = dω/dt )}$$

$$\mathrm{\overrightarrow{\tau}=\frac{d(\overrightarrow{I}\times \overrightarrow{\omega})}{dt}\:\:\:\:\:\:(\overrightarrow{L}=\overrightarrow{I}\times \overrightarrow{\omega})}$$

$$\mathrm{\overrightarrow{\tau}=\frac{d\overrightarrow{L}}{dt}}$$

旋转体的扭矩等于角动量相对于时间的变化率。这表示为牛顿旋转第二定律。

角动量的例子

角运动在物理学中的运动学中非常重要。角运动的应用非常广泛。以下是一些使用角动量的例子。

花样滑冰

在滑冰运动中，运动员应保持其角速度以保持稳定，从而形成不同的圆形路径图案。为了降低路径的角速度，他们伸展手臂，为了增加角速度，他们靠拢。

地球自转

地球自转是角动量的最佳例子。地球由于轨道角动量而绕太阳旋转。地球由于自旋角动量而绕自身轴旋转。

陀螺仪

它是一种基于角动量守恒原理来维持方向和角速度的设备。当施加外力时，陀螺轮的旋转轴保持在固定方向。它用于需要固定方向的空间。由于快速旋转产生的角动量使陀螺仪能够直立在其轴上。

结论

角动量是既具有大小又具有方向的矢量。角动量由粒子的速度和质量计算得出。其单位为$\mathrm{Kg\:m^2\:s^{−1}}$。右手定则最能解释角动量的方向。扭矩也是使物体绕轴旋转的矢量。角动量在日常生活中有着广泛的应用。地球自转是角动量的最佳例子。

常见问题

Q1. 动量和角动量有什么区别？

答。

线性动量	角动量
相对于参考点改变其位置的属性	相对于参考点改变其角度的属性。
公式 $\mathrm{\overrightarrow{p}=m\times \overrightarrow{v}}$	公式 $\mathrm{\overrightarrow{L}=\overrightarrow{I}\times \overrightarrow{\omega}}$
力 = 质量 x 线性加速度	扭矩 = 惯性矩 x 角加速度
只要施加恒力，它就是恒定的。	4. 只要施加恒定的扭矩，它就是恒定的。
$\mathrm{单位 - Kg\:m^2\:s^{−1}}$	$\mathrm{单位 - Kg\:m^2\:s^{−1}}$

表 1：线性动量和角动量的区别

Q2. 角动量守恒定律是什么？

答。除非对物体施加扭矩，否则物体的角动量是恒定的。这就是角动量守恒定律。

Q3. 跳水运动员在跳水前和跳水后会改变姿势。为什么？

答。在从跳水板跳水之前，跳水运动员会伸展他们的手和腿以保持较大的惯性矩。跳水后，他们会将手和腿收拢以减小惯性矩。因此，由于惯性矩较小，跳水运动员旋转得更快。再次，在到达水面时，他们伸展身体。

Q4. 花样滑冰运动员如何控制他们的速度？

答。旋转时，花样滑冰运动员伸展或收拢他们的手。他们这样做是为了降低或提高他们的旋转速度。

Q5. 用一个例子解释扭矩？

答。扭矩是旋转力。在我们家里打开和关闭水龙头时，我们施加了一个扭矩使其旋转。较短的把手更难打开，而较长的把手更容易打开。