角动量——绕固定轴旋转

---

引言

角动量是旋转动力学中的一个概念。我们可以将物体的运动分为两类，即平移运动和旋转运动。在纯平移运动中，物体上的每个点都在一条直线上运动。每个点在给定的时间间隔内移动相同的距离。例如，直线行驶的汽车、在大路上行走的行人等。而在纯旋转中，每个点的运动形成的路径形成一个圆，其圆心位于旋转轴上。例如，地球绕其轴自转、陀螺旋转等。

对于平移运动，在没有外力的作用下，我们会发现线性动量总是守恒的。我们称之为动量守恒定律。我们用它来简化许多碰撞问题。有人会问，旋转运动中是否存在这样的定律？答案是肯定的。在旋转运动中，我们有角动量守恒定律。角动量是线性动量的角对应值。正如我们所见，我们能够将它与转动惯量、力矩和线性动量等其它物理量联系起来。

角动量

假设一个质点绕一个轴旋转，那么质点绕该轴的动量矩被称为质点的角动量。

即角动量=线动量×质点的垂直距离

$$\mathrm{\overrightarrow{L}=\overrightarrow{p}\times \overrightarrow{r}}$$

质量为 m 的质点以速度 v 运动，则其线性动量为 L，假设其到旋转轴的距离由半径向量 $\mathrm{\overrightarrow{r}}$给出

角动量矢向量表示

$$\mathrm{\overrightarrow{L}= \overrightarrow{r}\times \overrightarrow{p}}$$

$$\mathrm{\lvert\overrightarrow{L} \rvert =rpsin\theta=mvr\:sin\theta}$$

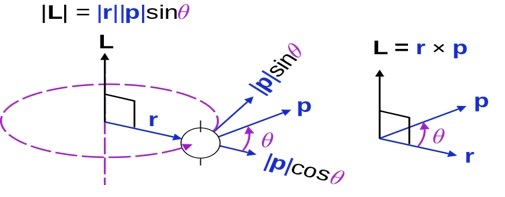
Maschen，角动量定义，标为公有领域，维基百科共享资源上有更详细的信息

角动量的单位为 $\mathrm{[ML^2 T^{-1}]}$，国际单位制单位为 $\mathrm{Kg\:m^2 s^{-1}}$。

直角坐标系中的角动量

我们还可以在笛卡尔坐标中明确写出角动量。首先，我们以笛卡尔形式写出 $\mathrm{\overrightarrow{r}}$和 $\mathrm{\overrightarrow{p}}$。

$$\mathrm{\overrightarrow{r}=x\hat{i}+y\hat{j}+z\hat{k}}$$

$$\mathrm{\overrightarrow{p}=p_x\hat{i}+p_y \hat{j}+p_z\hat{k}}$$

$$\mathrm{\overrightarrow{L}=(x\hat{i}+y \hat{j}+z\hat{k})\times (p_x\hat{i}+p_y\hat{j}+p_z\hat{k})}$$

$$\mathrm{\overrightarrow{L}_x=yp_z-zp_y}$$

$$\mathrm{\overrightarrow{L}_y=zp_x-xp_z}$$

$$\mathrm{\overrightarrow{L}_z=zp_y-yp_x}$$

角动量方程的推导

首先，我们来看平移运动和旋转运动的类似物理量。

量	速度	加速度	力	质量	动量
平移	$\mathrm{\overrightarrow{ u}}$	$\mathrm{\overrightarrow{a}}$	$\mathrm{\overrightarrow{F}}$	$\mathrm{m}$	$\mathrm{\overrightarrow{p}}$
旋转	$\mathrm{\overrightarrow{\omega}}$ (角速度)	$\mathrm{\overrightarrow{a}}$ (角加速度)	$\mathrm{\overrightarrow{\tau}}$(力矩) =$\mathrm{\overrightarrow{r}\times \overrightarrow{F}}$	I(转动惯量) = $\mathrm{Σmr^2}$	$\mathrm{\overrightarrow{L}}$(角动量)

表 1: 旋转运动和平移运动物理量的类比

我们取一个质量为 m 的小质点，其与旋转轴距离为 $\mathrm{\overrightarrow{r}}$，线性动量为 $\mathrm{\overrightarrow{p}}$。

根据牛顿第二定律，我们有

$$\mathrm{\sum \overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}}$$

我们对这个方程两边都与 r 做叉积。

$$\mathrm{\overrightarrow{r}\times \sum \overrightarrow{F}=\overrightarrow{r}\times \frac{d\overrightarrow{p}}{dt}}$$

我们意识到

$$\mathrm{\overrightarrow{r}\times \sum \overrightarrow{F}=\overrightarrow{\tau}}$$

因此

$$\mathrm{\overrightarrow{\tau}=\overrightarrow{r}\times \frac{d\overrightarrow{p}}{dt} ………. (1)}$$

现在我们来看这个式子

$$\mathrm{\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}}$$

因为

$$\mathrm{\overrightarrow{p}=m\overrightarrow{v}\:and\:\frac{d\overrightarrow{r}}{dt}=\overrightarrow{v};}$$

$$\mathrm{\overrightarrow{v}\times \overrightarrow{p}=m(\overrightarrow{v}\times \overrightarrow{v})=0}$$

（对于任何向量 $\mathrm{\overrightarrow{A}:\overrightarrow{A}\times \overrightarrow{A}=0}$）

因此，我们可以在方程 (1) 的两边添加它

$$\mathrm{\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}+\overrightarrow{\tau}=\overrightarrow{r}\times \frac{d\overrightarrow{p}}{dt}+\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}=\frac{d(\overrightarrow{r}\times \overrightarrow{p})}{dt}}$$

因此

$$\mathrm{\overrightarrow{\tau}=\frac{d(\overrightarrow{r}\times \overrightarrow{p})}{dt}}$$

如果我们将它与平移运动中的类似力进行比较

$$\mathrm{\sum F=\frac{dp}{dt}}$$

我们可以说项 $\mathrm{(\overrightarrow{r}\times \overrightarrow{p})}$ 是一种动量。

因此，我们定义角动量

$$\mathrm{\overrightarrow{L}=(\overrightarrow{r}\times \overrightarrow{p})}$$

刚体绕定轴的角动量

系统的角动量

设有一个由 n 个粒子组成的系统，它们的各个角动量由 $\mathrm{\overrightarrow{l_1},\overrightarrow{l_2},\overrightarrow{l_3},............\overrightarrow{l_n}}$ 表示，那么该系统的总角动量可以写为 -

$$\mathrm{\overrightarrow{L}=\overrightarrow{l_1}+\overrightarrow{l_2}+\overrightarrow{l_3}.................+\overrightarrow{l_n}=\sum_{i}\overrightarrow{L_i}}$$

$$\mathrm{\frac{d}{dt}(\overrightarrow{L})=\sum \frac{d}{dt} \overrightarrow{l_i}=\sum_i \overrightarrow{\tau_{ext,i}}}$$

因此，作用在系统上的总外力矩等于系统总角动量的变化率。

对于刚体

我们将刚体看作是一个由小粒子组成的巨大系统。设每个粒子的质量为 $\mathrm{m_i}$，线速度为 $\mathrm{\overrightarrow{v_i}}$。假设该物体绕 z 轴以角速度 $\mathrm{\overrightarrow{\omega_i}}$ 运动，并且粒子在 x-y 平面上围绕 z 轴旋转。

那么每个粒子的角动量

$$\mathrm{\overrightarrow{L_i}=m_i(\overrightarrow{r_i}\times \overrightarrow{v_i})}$$

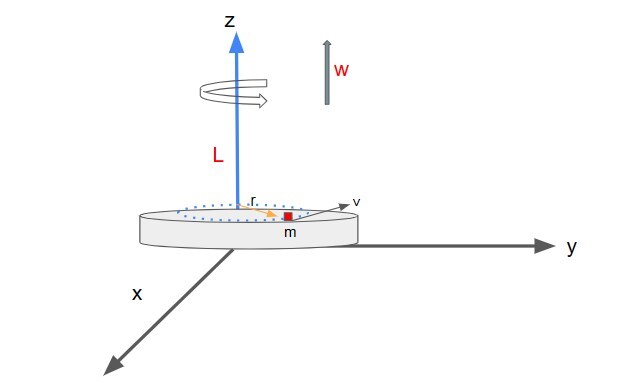
如图所示，$\mathrm{\overrightarrow{r_i}}$ 和 $\mathrm{\overrightarrow{v_i}}$ 之间的角度为 90°。

$$\mathrm{\Rightarrow\:\:\overrightarrow{L _i}=m_i(\overrightarrow{r_i}\times \overrightarrow{
u_i})= m_i\:r_i\:v_i\: sin90=m_i\:r_i\:v_i}$$

因此

$$\mathrm{\overrightarrow{L _z}=\sum \overrightarrow{L _i}=\sum m_i\:r_i\:v_i}$$

我们知道

$$\mathrm{
u_i=\overrightarrow{r_i\omega}}$$

所以

$$\mathrm{\overrightarrow{L_z}=\omega\sum m_i\:r_i^2=I \overrightarrow{\omega}}$$

since 惯性矩

$$\mathrm{I =\sum m_i\:r_i^2}$$

因此，对于刚体

$$\mathrm{\overrightarrow{L_z}=I \overrightarrow{\omega}}$$

即，刚体绕 z 轴的总角动量等于角动量和惯性矩的乘积。

我们知道 $\mathrm{\overrightarrow{\tau}=\frac{d\overrightarrow{L}}{dt}}$

因此

$$\mathrm{\overrightarrow{\tau}=\frac{d}{dt}(I\overrightarrow{\omega})=I\overrightarrow{\alpha}}$$

即，作用在刚体上的合力矩是其惯性矩和角加速度的乘积。

它为我们提供了力矩和角加速度之间的关系。它类似于牛顿第二定律

平移运动	$\mathrm{\overrightarrow{F}=m\overrightarrow{a}}$	$\mathrm{\overrightarrow{p}=m\overrightarrow{ u}}$
旋转运动	$\mathrm{\overrightarrow{\tau}=I\overrightarrow{\alpha}}$	$\mathrm{\overrightarrow{L}=I\overrightarrow{\omega}}$

表-2：牛顿第二定律在旋转和平移运动中

结论

角动量类似于旋转运动中的线动量。它取决于与旋转轴的距离。角动量只有在围绕特定原点定义时才有意义。它是一个矢量量，总是垂直于 $\mathrm{\overrightarrow{r}}$ 和 $\mathrm{\overrightarrow{p}}$的平面。角动量变化率给我们粒子上的力矩。我们还可将此概念用于多粒子系统。对于刚体，它等于该物体的角速度乘以惯性矩。我们还可以展示旋转运动和平移运动之间的对应关系，如表-1 中总结的那样。

常见问题

Q1. 角动量守恒的条件是什么？

问题：孤立系统的角动量始终守恒，前提是外部扭矩为零。即 $\mathrm{\overrightarrow{\tau_{ext}}=0}$

问题 2：角动量的物理意义是什么？

回答：角动量在物理上是物体转动运动的度量，而扭矩是力转动效应的度量。

问题 3：圆周运动中粒子的线动量始终在变化，这是否也适用于角动量？

回答：对于圆周路径上的粒子，$\mathrm{\overrightarrow{L}=(mvr)\hat{k}}$ 因此，如果粒子绕着穿过其中心的轴运动，则角动量不会改变。

问题 4：非旋转物体是否可以拥有角动量？

回答：是的，假设一个粒子沿着直线上某条路径运动，如果我们取 O 点为轴，如果 O 点偏离那条直线，那么我们会得到非零角动量。因为 $\mathrm{\overrightarrow{r}\times \overrightarrow{v}}$ 将非零。

问题 5：一个球体和一个相同质量的圆柱体绕着相同的轴线以相同角速度旋转，哪个物体将具有更大的角动量？

回答：圆柱体的转动惯量 > 相同质量的球体的转动惯量。

因此圆柱体的角动量 > 球体的角动量