角频率

---

引言

根据物理学术语，角频率定义为单位时间内角位移的量度。为了更好地解释这个概念，本文包含了角频率的适当定义和示例。侧重于波的协调，角频率公式的推导包含了角位移变化率。

什么是角频率？

当一个物体或一个物体被释放绕给定轴旋转时，该物体开始进行角振荡。这种振荡产生物体的角位移速度，其定义基于类似于物体角位置变化的段的运动。

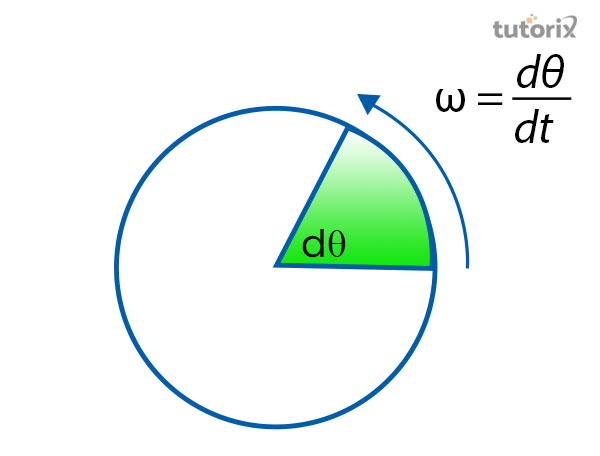
图1：产生角频率的角位移

• 基于此概念，角频率通常被称为圆频率或径向频率，包括基于每个时间单位的角位移的测量。
• 以弧度每秒表示的周期性过程的频率被认为等于基于每个时间单位充电的正弦波形 (Abouelregal & Marin, 2020)。
• 这个旋转物体的频率通常基于单位时间内事件重复的次数来测量。

波的角频率

旋转物体的频率被定义为物体的特定状态，它以波在单位时间内通过某一点的完整周期数来表示。为了确定次数，需要确定波是否通过单个点。

因此，波的角频率的测量包括波的完整周期通过某一点所需的时间周期。基于这个特定概念，角频率被称为位于波运动中的任何粒子的角位移，该粒子根据每个时间单位穿过稳定点。

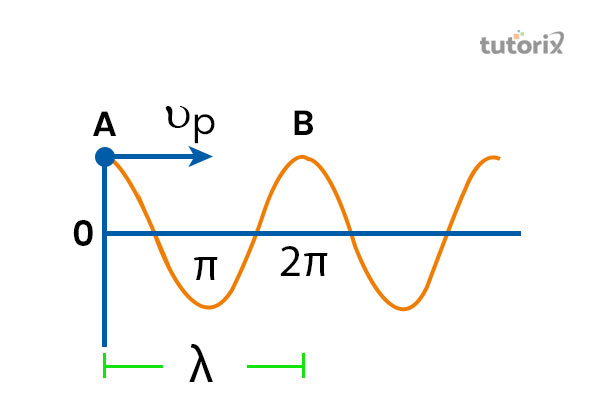
图2：波的角频率

考虑到上图，可以看出，谐波波沿特定弦的一个元素的位移朝着相对于时间固定的特定方向移动。

为了确定波的角频率，必须记住弦元素通过保持简谐运动上下移动。

角频率与时间的关系

用特定字母 T 表示，它表示旋转物体基于轴完成单次旋转所需的时间量。在表示为波动的振动的情况下，周期被认为是振动通过稳定点所需的时间量 (Wardani, 2020)。

这些属性，如周期和角频率，共享一个由以下等式表达的数学关系。

T = 2m/qB

在这个等式中，m 代表电子的质量，q 代表电荷，而 B 代表“宗教中的磁场”。另一方面，旋转物体的周期由以下等式表示：

T = 1/f

在这个等式中，f 代表频率，T 代表周期。

角频率公式

旋转频率是指物体在一定时间内完成的旋转次数。为了表示角频率的计算，推导出的公式是 f = 1/T (Wardani, 2020)。为了找到地球的角旋转，考虑的周期是 365 天。确定这一事实后，计算地球角频率的公式是

f = 1/365

在某些情况下，角频率公式表示为“ω = 2πf”，其中角频率与运动物体的振荡频率相关，该频率乘以物体通常形成旋转轨道的特定角度。

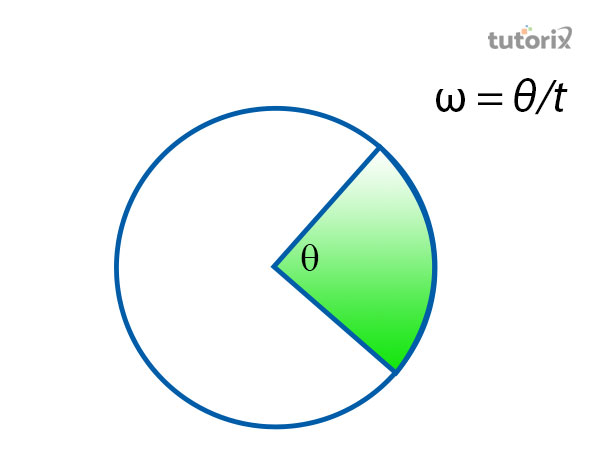
图3：角频率

基于这个特定概念，形成了一个通用的公式：

ω = θ/t

这个特定概念在上图中表示。在上图的上下文中，θ被认为是旋转物体确定的角度，t 代表移动物体穿过特定角度 θ 所用的时间。

角频率示例

为了通过示例理解公式，假设一个人坐在摩天轮的顶部。这个人观察到轮子在 15 秒内完成了四分之一的旋转。在这种情况下，有两种方法可以找出摩天轮的角频率。

根据第一个公式，如果考虑四分之一旋转需要 15 秒的条件，则车轮的完整旋转将在 (4*15=) 60 秒内完成。

基于此，旋转频率 f 将等于 1/60s^-1，因此角频率将为 ω = 2πf，等于 π/30。

其次，坐在轮子顶上的人在 15 秒内移动 π/2 弧度，这导致 ω = (π/2)/15 的公式，等于 π/30。

结论

旋转物体的标量通常由角频率定义。已经观察到，角频率的公式取决于诸如周期之类的属性，周期被称为物体获得速度和角位移的特定轴。基于计算物体每单位时间旋转或通过固定轴的频率有助于推导出公式 ω=2πf

常见问题

Q1. 频率和角频率有什么区别？

旋转物体单位时间内完成的圆周数定义了频率，在物体的圆周运动中观察到的角位移被称为角频率。

Q2. 弹簧的角频率取决于什么？

弹簧的角频率通常基于对象的合力与电子质量，而不是振幅。

Q3. 角频率是否与弹簧常数相关？

物理学中确定物体的角频率是常数，因此弹簧的角频率取决于物体的质量和弹簧常数。

Q4. 角速度和频率有什么区别？

角速度等于频率和常数 2π 的乘积，而角频率定义为单位时间的旋转速度。

参考文献

期刊

Abouelregal, A. E., & Marin, M. (2020). The size-dependent thermoelastic vibrations of nanobeams are subjected to harmonic excitation and rectified sine wave heating. Mathematics, 8(7), 1128. Retrieved from: https://www.mdpi.com

Wardani, F. (2020, April). An analysis of student's concepts understanding about simple harmonic motion: Study in vocational high school. In Journal of Physics: Conference Series (Vol. 1511, No. 1, p. 012079). IOP Publishing. Retrieved from: http://repo.unida.gontor.ac

网站

En.universaldenker.org, (2022). Phase Velocity of a Wave. Retrieved from: https://en.universaldenker.org [Retrieved on: 7th June 2022]

Lambdageeks.com，(2022)。简谐运动的角频率：详尽的见解。检索自：https://lambdageeks.com [检索日期：2022年6月7日]