角加速度

---

简介

角加速度是旋转动力学中的一个概念，就像加速度在直线运动中被定义一样。从物理上讲，它描述了粒子角速度的变化率。由于旋转运动是围绕某个轴或点进行的，因此角加速度根据我们原点的选择具有不同的值。

角加速度可能是由外力矩引起的，也可能是由于物体结构的变化而引起的，而没有任何外部影响。后一种情况的一个常见例子是，坐在旋转椅子上的人在将手臂向内拉时获得角速度。

什么是角加速度？

角加速度是线性加速度的旋转对应物。从数学上讲，它被定义为角速度对时间的导数，通常用希腊字母 alpha (α) 表示。角加速度是一个矢量量，其方向垂直于粒子的运动平面。

角加速度单位

我们知道物体的角位置用弧度来衡量，因此角速度用弧度每秒来衡量。由于角加速度是此量的变化率，因此它的单位可以很容易地推导出来。

因此，在 SI 系统中，角加速度的单位是弧度每秒平方 (rad/s2)，对应于维度 $\mathrm{T^{−2}}$。

角加速度公式

考虑一个物体，其角位置和角速度分别用 theta $\mathrm{(\theta)}$ 和 omega $\mathrm{(\omega)}$ 表示。角加速度最简单的公式表示为角速度对时间的导数。

$$\mathrm{\alpha=\frac{d\omega}{dt}}$$

此外，由于角速度本身取决于角位置，我们还有

$$\mathrm{\alpha=\frac{d^2\theta}{dt^2}}$$

角加速度也可以通过将最终和初始角速度之间的差除以相应的时间变化来估计。

$$\mathrm{\alpha=\frac{\omega_2-\omega_1}{t_2-t_1}=\frac{\Delta \omega}{\Delta t}}$$

角加速度示例

1. 一块石头被绑在拉紧的绳子上，在 15 秒内达到 30 rad/s 的角速度。求石头的角加速度。

答案：已知石头在 15 秒内达到 30 rad/sec 的角速度。

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}=\frac{30-0}{15-0}=\frac{30}{15}=2\:rad/sec^2 }$$

2. 物体的角旋转由方程 $\mathrm{\theta=3t^4+6t^2-7t+2}$ 给出。求其在 t=7 秒时的角加速度。

答案：使用公式

$$\mathrm{\alpha=\frac{d^2\theta}{dt^2}}$$

$$\mathrm{\alpha=\frac{d^2}{dt^2}(3t^4+6t^2-7t+2)=36t^2+12}$$

在 t=7 秒时

$$\mathrm{\alpha=36×(7)^2+12=1776\:rad/s2}$$

角加速度的应用

加速汽车的车轮

当我们加速或减速汽车时，车轮的角速度相应地增加或减少。也就是说，车轮会受到角加速度，角加速度与汽车的线性加速度通过以下公式关联

$$\mathrm{\alpha=\frac{a}{r}}$$

吊扇

吊扇起初转速缓慢，但很快达到所需的转速。也就是说，它的角速度在达到某个值之前会增加。因此，其运动与角加速度相关。请注意，由于风扇绕其轴旋转，因此这与前一个示例一样，是自旋角加速度的一个示例。

角加速度类型

旋转运动下可能存在两种类型的运动。

自旋角加速度

刚体可以绕穿过它的轴旋转，从而产生粒子的所谓的自旋。一个常见的例子是板球中的旋转球。

与这种类型的运动相关的角加速度称为自旋角加速度。

轨道角加速度

另一方面，任何物体，无论是刚性物体还是其他物体，都可以围绕一个点进行运动，从而产生某种轨道运动。想象这种运动的最简单方法是观察行星运动。所有行星都以椭圆轨道绕太阳运行，因此具有轨道运动。这种类型的运动涉及轨道角加速度。

一个物体也可能同时具有自旋和轨道运动。地球的同时自转和公转是这种情景的一个非常简单的例子。

点粒子的轨道角加速度：二维

在二维情况下，当物体相对于一个点运动时，它可能具有角加速度。这被称为它的轨道角加速度，等于轨道角速度的瞬时变化率。

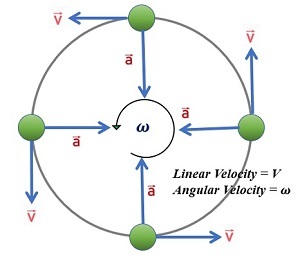
此图中的绿色箭头表示粒子瞬时速度的切向分量，而紫色箭头表示角速度。

$$\mathrm{v=r\omega}$$

$$\mathrm{\omega=\frac{v}{r}}$$

我们知道

$$\mathrm{\alpha=\frac{d\omega}{dt}=\frac{d}{dt}(\frac{v}{r})}$$

要解决此问题，请应用微积分中的乘积法则。我们将得到

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{v}{r^2}(\frac{dr}{dt})}$$

这是点粒子在二维中的轨道角加速度。

特殊情况：如果粒子正在执行圆周运动，这意味着半径随时间保持不变。因此，角加速度写成

$$\mathrm{alpha=\frac{1}{r}\frac{dv}{dt}}$$

角加速度与线性加速度之间的关系

我们再次从推导出角加速度的公式开始。为此，考虑一个以线性速度 v 运动的物体。然后，角速度为

$$\mathrm{\omega=\frac{v}{r}}$$

因此，

$$\mathrm{\alpha=\frac{d\omega}{dt}=\frac{d}{dt}(\frac{v}{r})}$$

使用乘积法则，

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{v}{r^2}(\frac{dr}{dt})}$$

当粒子的半径不恒定时，角加速度和线性加速度之间的关系难以制定。

但是，当半径保持不变时，

$$\mathrm{\frac{dr}{dt}=0}$$

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}}$$

因此，

$$\mathrm{\alpha=\frac{a}{r}}$$

角加速度公式

物体的角加速度可以通过以下任何公式获得 -

$$\mathrm{\alpha=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2}}$$

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}-\frac{v}{r^2}\frac{dr}{dt}}$$

当运动是圆周运动时，

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{a}{r}}$$

解答题

Q1. 物体的角速度在 0.75 秒内从 $\mathrm{\frac{\pi}{4}}$ rad/s 变为 $\mathrm{\frac{3\pi}{8}}$ rad/s。求其角加速度。

答。使用

$$\mathrm{\alpha=\frac{\Delta\omega}{\Delta t}}$$

我们有

$$\mathrm{\alpha=\frac{\frac{3\pi}{8}-\frac{\pi}{4}}{0.75}=\frac{\frac{\pi}{8}}{0.75}=\frac{\pi}{6}\:rad/s^2}$$

Q2. 粒子的角加速度为 3 rad/s²。如果它从静止开始，求其经过 46 弧度距离后的角速度。

答。设 $\mathrm{\omega_1}$ 和 $\mathrm{\omega_2}$ 为粒子的初始和最终角速度，θ 为所经过的距离。

运动方程为 $\mathrm{\omega_2^{2}-\omega_2^{1}=2\alpha \theta}$

这里，粒子从静止开始，因此，$\mathrm{\omega_1=0}$。

因此，

$$\mathrm{\omega_2=\sqrt{2\alpha \theta}=\sqrt{2\times 3\times46}=\sqrt{276}=16.61 rad/s.}$$

结论

角加速度是线性加速度的旋转对应物，由角速度的变化率给出。它的值根据原点的选择而变化，因此，即使是直线运动的粒子也可能具有角加速度。对于圆周运动，角加速度由 $\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{a}{r}}$ 给出 运动方程对于旋转情况和线性情况同样有效。

常见问题

Q1. 直线运动的粒子是否具有角加速度？

答。是的。根据所选原点，粒子的角速度可能不是恒定的，因此可能存在角加速度。

Q2. 运动方程对于旋转动力学是否有效？

答。是的，略有修改。旋转情况下的运动方程如下所示。请注意，为了使这些方程成立，角加速度必须是均匀的。

• $\mathrm{\omega_2^{2}-\omega_1^{2}=2\alpha\theta}$

• $\mathrm{\omega_2=\omega_1+\alpha t}$

• $\mathrm{\theta=\omega_1 t+\frac{1}{2} \alpha t^2}$

Q3. 角加速度的方向是什么？

答。角加速度矢量指向垂直于运动平面的方向。如果角速度沿逆时针方向增加，则其符号为正，否则为负。

Q4. 地球是否具有任何角加速度？

答。地球绕其轴的角加速度几乎为零。有各种因素导致地球角速度发生无限小的变化，但与地球的实际角速度（大约每天 2π 弧度）相比，这些变化太小了。

Q5. 当粒子在三维空间中运动时，轨道角加速度是多少？

答。在三维空间中，角速度表示为

$$\mathrm{\omega=\frac{r×v}{r^2}}$$

对时间求导，我们得到

$$\mathrm{\alpha=\frac{r\times a}{r^2}-\frac{2}{r}\frac{dr}{dt}\omega}$$

Q6. 简谐振子的角加速度是多少？

答。对于简谐振子，运动方程为 $\mathrm{\ddot{\theta}=-\frac{g}{R}\:sin\:\theta}$ 。这是简谐振子在与垂直方向成 θ 角的瞬时所经历的角加速度的值。