恒定角加速度

---

引言

恒定角加速度是旋转动力学中的一个重要概念。在描述线性速度变化时，我们使用线性加速度；然而，当处理旋转体或曲线运动的物体时，我们使用角加速度。角加速度是线性加速度的旋转对应物，如同角速度是旋转速率一样，这并不令人意外。与定义角速度变化率的角加速度相反，线性加速度解释了线性速度的变化率。

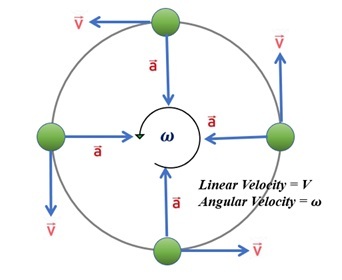
什么是角加速度？

角速度随时间的变化率称为角加速度。它是一个三维伪矢量。在国际单位制中，我们将其定义为弧度/秒平方(rad/sec²)。此外，我们通常用希腊字母'α’表示它。

有趣的是，角加速度既不是真正的矢量，也不是真正的标量。这意味着它像标量一样运作，因为它只需要一个大小就能完全定义，但根据你观察的方向，它可能会改变符号。

如何确定角加速度？

借助角加速度，我们可以修改由时间变化分隔的角速度。利用这一点可以很容易地获得正常的角加速度。角加速度将其运动方向指向枢轴方向。为了获得角加速度的程度，我们使用一个方程，

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}=\frac{\omega_2-\omega_1}{t_2-t_1}}$$

旋转物体的角加速度是指角速度变化相对于所用时间的频率。它是隔离角速度变化的时间变化。角速度的变化除以时间的变化就是正常的角加速度。

什么导致角加速度？

加速度与运动有关，无论是角运动还是线性运动。因此，我们知道运动总是由力驱动的。所以，角加速度也有一个力源导致它。

当旋转一个扩展物体（例如其质量分散在空间中的杆、圆盘或立方体）时，我们必须考虑力的位置。

力矩是衡量力启动旋转能力的指标。根据物理学原理，作用于物体的力矩取决于所施加力的位置和大小。当我们考虑力矩（导致旋转加速度）时，你从力的严格线性概念（作为沿直线作用的实体）转移。

力矩是一个矢量量。力矩的大小提供了关于其产生旋转能力的信息；更准确地说，力矩的大小与它产生的角加速度成反比。力矩沿角加速度的轴施加。

一些与角加速度相关的重要的术语

当我们研究角运动时，角加速度是一个非常重要的术语。这里还有一些与角加速度相关的术语。

角动量

刚体的动量是通过将其转动惯量乘以其角速度来计算的。如果没有外力作用于物体上，它就像线性动量一样，遵循动量守恒原理的基本规则。它可以从粒子的动量表达式推导出来。

$$\mathrm{L=I×ω}$$

力矩

使物体绕轴旋转的力称为力矩。几乎就像力在直线力学中加速物体一样，力矩在角方向上加速物体。

力矩也是一个矢量量。作用于轴上的力定义了力矩矢量的方向。

$$\mathrm{\tau=F.r}$$

角速度

物体的旋转速率和方向都由其角速度描述。逆时针方向通常被视为正方向。旋转速率的矢量表示，或物体相对于另一点旋转或旋转的速度，称为角速度。

$$\mathrm{\omega=\frac{\theta}{t}}$$

角加速度的一些实际应用

物理学中的每一个术语在我们的日常生活中都非常适用。在这里，我们将学习角动量的应用。

• 子弹射出膛线枪管时，膛线会刻在子弹上，使其旋转。

• 当四分卫用手指旋转投球时，足球在空中快速旋转。紧密的螺旋形是球迷们识别好球的方式。

• 刻在枪管上的膛线形成了围绕枪口出口孔的吸引人的螺旋图案。

结论

角加速度是线性加速度的旋转等效物。与定义角速度变化率的角加速度相反，线性加速度解释了线性速度的变化率。

根据传统观点，正角加速度会使旋转加速到逆时针方向，而负角加速度会使旋转加速到顺时针方向。角加速度的SI单位是弧度每秒平方。

我们用角速度的变化除以时间的变化来确定物体的角加速度。这得到角加速度或每秒角速度的平均变化。

常见问题

Q1. 角加速度的正负号有何意义？

A1. 角加速度的大小是一个正数。但是，我们观察到角加速度的大小带有正负号。这些符号对于角加速度的方向非常重要。当角速度逆时针增加时，角加速度的符号被认为是正的；当它顺时针增加时，它被认为是负的。

Q2. 角动量对我们有什么重要性？

A2. 在角速度的背景下，角加速度是角度变化率；其大小和方向分别提供关于变化率和方向的信息。

Q3. 我们有一个吊扇，它通过将模式从低速切换到高速来开始加速。风扇叶片的加速度为 1.5 rad/s²，持续 2 秒。如果初始角速度为 4 rad/s，现在计算风扇的最终角速度。

A3. 我们知道角加速度是

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}}$$

现在，我们有

初始速度 = 4 rad/s

角加速度 = 1.5 rad/s²

因此，使用角加速度方程

$$\mathrm{\alpha \Delta t=\Delta \omega}$$

$$\mathrm{\alpha \Delta t=\omega_f-\omega_i}$$

因此，

$$\mathrm{\omega_f=\alpha \Delta t+\omega_i}$$

$$\mathrm{\omega_f=1.5×2+4}$$

$$\mathrm{\omega_f=7\:rad/s^2}$$

Q4. 我们有一个正在旋转的牛顿盘。然而，它以 50 rad/s 的速度改变了旋转速度。圆盘的速度变化持续 7 秒。现在，评估牛顿圆盘的角加速度大小。

A4. 根据定义，我们知道角加速度是速度变化与时间的比率。

因此

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}}$$

$$\mathrm{\alpha=\frac{50}{7}}$$

$$\mathrm{\alpha=7.14\: rad/s^2}$$