地球角速度

---

简介

角速度是一个标量。包含大小和方向的物理量称为矢量量，例如位移、速度等。仅包含大小的物理量称为标量。例如，距离、速度等。

角速度和角速度都用相同的公式表示，但它们之间唯一的区别是角速度是矢量量，而角速度是标量。圆周运动是角运动的一个例子，因为在每个点上，运动物体相对于时间在其每个点上都改变了它们的角。

角运动

如果粒子相对于时间改变其位置，则表示它处于运动状态。如果粒子的运动沿着直线，则称为线性运动。如果粒子的运动是沿着圆形路径，则称为圆周运动或轨道运动或角运动。地球的自转、铁饼投掷、绳子系住的石头的运动都是旋转或角运动的一些例子。因此，角运动定义为任何围绕固定点运动的物体。

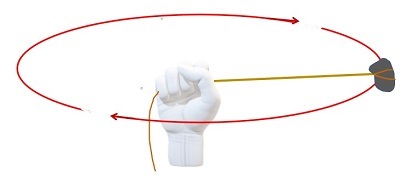
什么是角速度？

角速度公式：经历圆周运动的粒子的角速度由它完成路径的速度决定。角速度是完整旋转中角度随时间的变化。它也用符号 ω 表示。

$$\mathrm{ω=\frac{2\pi}{t}}$$

速度是用来了解物体运动快慢的术语。因此，角速度是旋转物体速度的度量。

角速度单位：弧度每秒。

角速度作为向量场

角速度是在向量场中，它恰好是线性速度 v 的向量场的旋度的值的一半。

$$\mathrm{\overrightarrow{\omega}=\frac{1}{2}(\overrightarrow{
abla}\times \overrightarrow{
u})}$$

角速度公式

角速度由物体在特定时间内完成一次完整旋转所经过的总角距离计算得出。

$$\mathrm{\overrightarrow{\omega}=\frac{2\Pi}{t}}$$

ω - 角速度

t - 完成一次完整旋转所需的时间

它也可以通过使用以下公式从线性速度计算得出：

$$\mathrm{
u=r\omega}$$

地球的角速度

我们的地球绕着自己的轴自转，给我们带来昼夜交替。地球完成一次完整旋转所需的时间是 23 小时 56 分 4.09 秒。完整旋转的角位移为 2π 弧度。

$$\mathrm{角速度=\frac{角位移}{完成一次旋转所需时间}}$$

为此，时间应转换为秒。

$$\mathrm{1小时=60分钟= 3600秒}$$

$$\mathrm{23小时=23×3600=82800秒}$$

$$\mathrm{1分钟 = 60秒}$$

$$\mathrm{56分钟=56×60=3360秒}$$

完成一次完整旋转所需的时间 = 82800 + 3360 + 4.09 = 86164.09

$$\mathrm{角速度=\frac{2\Pi}{86164.09}}$$

$$\mathrm{
u=\frac{6.28}{86164.09}}$$

$$\mathrm{角速度\
u=7.28×10^{-5} 弧度/秒}$$

角速度示例

1. 如果风扇叶片以 16π 弧度/秒的角速度旋转。它完成一次旋转需要多少时间？

答：我们知道

$$\mathrm{角速度=\frac{角位移}{时间}}$$

$$\mathrm{\omega=\frac{\theta}{t}}$$

给定

角速度 ω=16Π 弧度/秒

一次旋转的角位移 = 2π 弧度

$$\mathrm{t=\frac{\theta}{\omega}}$$

$$\mathrm{t=\frac{2\Pi}{16\Pi}}$$

$$\mathrm{t=0.125秒}$$

2. 半径为 2 米的汽车车轮以每秒 8 米的速度行驶。然后求角速度。

给定

线速度 $\mathrm{
u=8m/s}$

$$\mathrm{r=2m}$$

角速度

$$\mathrm{\omega=\frac{
u}{r}}$$

$$\mathrm{\omega=\frac{8}{2}=4弧度/s}$$

角速度和线速度之间的关系

角速度是根据线速度计算的。

粒子的线速度 $\mathrm{
u=\frac{ds}{dt}}$

粒子的角速度 $\mathrm{\omega=\frac{d\theta}{dt}}$

将方程两边乘以 r，我们得到：

$$\mathrm{r\omega=r\frac{d\theta}{dt}\:\:\:\:\:(rd\theta=ds)}$$

$$\mathrm{r\omega=\frac{ds}{dt}}$$

$$\mathrm{r\omega=
u}$$

将速度和角速度联系起来的方程是 $\mathrm{
u=r\omega}$

它可以修改为计算角速度为 $\mathrm{\omega=\frac{
u}{r}}$

结论

角速度是一个既有大小又有方向的矢量量。如果粒子沿圆形路径运动，则为圆周运动，物体具有的速度为角速度。角速度或角速度由物体在一分钟内产生的角位移计算得出。线速度和角速度相互关联。

常见问题解答

Q1. 赤道处的地球角速度是多少？

答。赤道处地球的速度为 $\mathrm{7.367×10^{-5}\frac{rad}{sec}}$

Q2. 我们如何计算角速度？

答。角速度由物体在特定时间内完成一次完整旋转所经过的总角距离计算得出。

$$\mathrm{\omega=\frac{2\Pi}{t}}$$

ω - 角速度

t - 完成一次完整旋转所需的时间

它也可以通过使用以下公式从线性速度计算得出：

$$\mathrm{
u=r\omega}$$

角速度以弧度/秒为单位计算。

Q3. 角速度在所有点都相同。解释原因？

答。角速度是角运动中单位时间内位移变化率，位移变化率相同。因此，角速度在所有点都相同。

Q4. 描述角速度和角速度。

答。速度是一个标量，因此角速度是对运动物体的标量估计。而角速度是对运动物体的矢量估计。角速度指定运动物体的大小和方向。

Q5. 花样滑冰运动员如何控制他们的角速度？

答。花样滑冰运动员和芭蕾舞演员在表演时会改变他们的速度。当他们伸展他们的手和腿时，它会增加惯性矩，从而降低角速度。

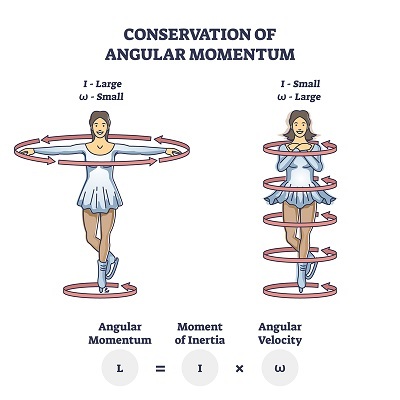
同样，当他们将手和腿靠近身体时，会减少惯性矩，从而角速度增加。这就是他们在表演过程中控制速度的方式。