互感：定义与公式

当两个线圈以这样一种方式布置，即一个线圈中电流的变化会导致另一个线圈中感应出电动势时，则称这两个线圈具有互感。互感用字母M表示，单位为亨利。

考虑两个线圈，线圈1和线圈2彼此相邻放置。当电流I1流过线圈1时，会在其中产生磁通量(Φ₁)，并且Φ₁的一部分与线圈2耦合，称为互通磁通量(Φ_m)。

现在，如果线圈1中的电流发生变化，则互通磁通量也会发生变化，因此在线圈2中会感应出电动势。线圈2中感应出的这种电动势称为互感电动势(𝑒_𝑚)。这种互感电动势是线圈之间互感的原因。互感的效果是根据线圈的布置增加或减少两个线圈的总电感。

互感公式

两个线圈之间的互感(M)可以通过以下三种方法中的任何一种确定，具体取决于已知量−

方法1

如果知道一个线圈中互感电动势(𝑒_𝑚)的大小以及另一个线圈中电流的变化率，则互感(M)由下式给出，

$$\mathrm{e_{m}=M\frac{dl_{1}}{dt}}$$

$$\mathrm{\Rightarrow\:M=\frac{e_{m}}{(dl_{1}/dt)}\:\:\:...(1)}$$

方法2

考虑两个磁耦合线圈，线圈1和线圈2，分别具有N₁和N₂匝。如果电流I₁流过线圈1，则会产生互通磁通量(Φ_m)，该磁通量与线圈2耦合。因此，

$$\mathrm{{m}=M\frac{dl_{1}}{dt}=\frac{d}{dt}(Ml_{1})}$$

此外，互感电动势由下式给出，

$$\mathrm{e_{m}=N_{2}\frac{d\phi_{m}}{dt}=\frac{d}{dt}(N_{2}\phi_{m})}$$

因此，通过将这两个方程相等，我们得到，

$$\mathrm{Ml_{1}=N_{2}\phi_{m}}$$

$$\mathrm{\Rightarrow\:M=\frac{N_{2}\phi_{m}}{l_{1}}\:\:\:...(2)}$$

方法3

如果已知磁路的物理尺寸，则可以如下确定其互感−

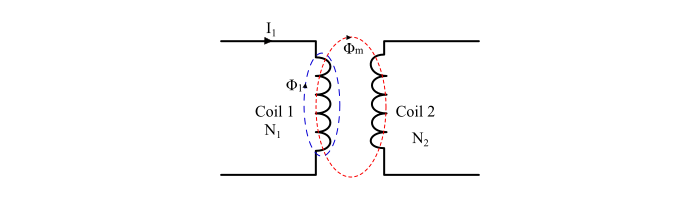
设‘l’和‘a’分别为磁路的长度和横截面积。N₁和N₂分别是线圈1和线圈2的匝数。

互通磁通量，

$$\mathrm{\phi_{m}=\frac{MMF}{Reluctance(s)}=\frac{N_{1}l_{1}}{(1/\mu_{0}\mu_{r}a)}}$$

其中，

• μ_𝑟 = 磁路材料的相对磁导率，

• μ₀ = 真空或空气的绝对磁导率。

$$\mathrm{\Rightarrow\:\frac{\phi_{m}}{l_{1}}=\frac{N_{1}}{(1/\mu_{0}\mu_{r}a)}}$$

$$\mathrm{(\because\:M=\frac{N_{2}\phi_{m}}{l_{1}})}$$

$$\mathrm{M=N_{2}(\frac{N_{1}}{1/\mu_{0}\mu_{r}a})}$$

$$\mathrm{\Rightarrow\:M=(\frac{N_{1}N_{2}}{1/\mu_{0}\mu_{r}a})=\frac{{N_{1}N_{2}}}{Reluctance(S)}\:\:\:\:...(3)}$$

方法4

如果两个线圈的自感分别为L1和L2，则互感也可以表示为，

$$\mathrm{M=k\sqrt{L_{1}L_{2}}\:\:\:...(4)}$$

其中，k是耦合系数。

Manish Kumar Saini

更新于: 2021年7月5日

1K+ 浏览量

启动你的职业生涯

通过完成课程获得认证

开始学习