数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究带点规约的互感
当自感和互感同时产生感应电动势时，在进行任何电路计算之前，必须确定这两个感应电动势的相对极性。线圈中由于互感产生的感应电动势，可能会根据绕组的意义和线圈中电流的方向，帮助或阻碍由于自感产生的感应电动势。
点符号或点规约
点规约或点约定可以表述如下：
如果两个电流都进入耦合线圈的带点端，或者两个电流都进入不带点端，则互感 (M) 的符号与自感 (L) 的符号相同。
如果一个电流进入带点端，另一个电流进入不带点端，则互感 (M) 的符号与自感 (L) 的符号相反。
解释
如果两个电流都流入每个点或流出每个点，则互感 (M) 为正。另一方面，如果一个电流流入带点端，另一个电流离开带点端，则互感 (M) 为负。
考虑以下电路示例：
互感 (M) 为正，因为电流 $I_{1}$ 和 $I_{2}$ 都流入点。
M 为正，因为电流 $I_{1}$ 和 $I_{2}$ 都流出点。
M 为负，因为电流 $I_{1}$ 流入点，而电流 $I_{2}$ 流出点。
耦合电感的电路方程
以下电路示例说明了耦合电路的电路方程的编写方法。
电路 1
考虑一个由两个电感 $L_{1}$ 和 $L_{2}$ 组成的耦合电路。设 $V_{1}$ 和 $V_{2}$ 是分别施加到电感的电压。假设两个电流 $I_{1}$ 和 $I_{2}$ 都进入带点端。因此，互感 (M) 的符号为正。
通过应用 KVL，电压方程可以写成：
$$\mathrm{V_{1}=L_{1}\frac{di_{1}}{dt}+M\frac{di_{2}}{dt}\:\:\:\:\:\:...(1)}$$
$$\mathrm{V_{2}=L_{2}\frac{di_{2}}{dt}+M\frac{di_{1}}{dt}\:\:\:\:\:\:...(2)}$$
电路 2
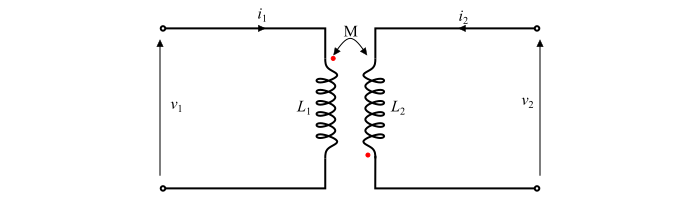
考虑一个由两个电感 $L_{1}$ 和 $L_{2}$ 组成的耦合电路。设 $V_{1}$ 和 $V_{2}$ 是分别施加到电感的电压。假设电流 $I_{1}$ 进入带点端，而电流 $I_{2}$ 离开带点端。因此，互感 (M) 的符号为负。
11K+ 浏览量
