数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学Python中的平衡二叉树
在二叉树中，每个节点包含两个子节点，即左子节点和右子节点。假设我们有一个二叉树，我们需要检查该树是否平衡。如果左子树和右子树的高度差小于或等于“1”，则称二叉树为平衡树。
示例
输入-1：
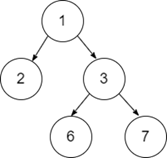
输出
True
解释
给定的二叉树是 [1,2,3, NULL, NULL, 6, 7]。其左子树和右子树的高度差等于“1”，因此它是一个高度平衡树。
输入-2：
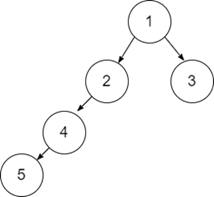
输出
False
解释
给定的二叉树是 [1,2,3,4, NULL, NULL,NULL,5]。其左子树和右子树的高度差大于“1”，因此它不是高度平衡树。
解决此问题的方法
解决此问题的递归方法是找到左子树和右子树的高度，然后检查 (height(leftsubstree) - height(rightsubtree) <= 1)，并根据情况返回 True 或 False。然后，我们将递归地检查二叉树的每个节点。
- 输入二叉树的节点。
- 定义一个函数来查找树的高度。
- 一个布尔函数，递归地检查左子树和右子树的高度差是否不超过“1”，然后返回 True。
- 返回结果。
示例
class treenode:
def __init__(self, data):
self.data = data
self.left = self.right = None
# funtion to find the height of the left subtree and right subtree
class height:
def __init__(self):
self.height = 0
# function to check if the tree is balanced or not
def isBalanced(root):
lh = height()
rh = height()
if root is None:
return True
return (
(abs(lh.height - rh.height) <= 1)
and isBalanced(root.left)
and isBalanced(root.right)
)
root = treenode(1)
root.left = treenode(2)
root.right = treenode(3)
root.left.left = None
root.left.right = None
root.right.left = treenode(6)
root.right.right = treenode(7)
if isBalanced(root):
print("Balanced")
else:
print("Not Balanced")运行以上代码将生成以下输出：
输出
Balanced
给定的二叉树 [1, 2, 3, NULL, NULL, 6, 7]。其左子树和右子树的高度差等于“1”，因此它是一个高度平衡树。
更新于：2021年2月23日
4K+ 浏览量
广告