数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++程序中的二分查找？
二分查找，也称为半区间搜索、对数搜索或二分法，是一种搜索算法，用于在一个已排序的数组中查找目标值的位置。二分查找将目标值与数组的中间元素进行比较。如果它们不相等，则排除目标值不可能存在的半部分，并在剩余的半部分继续搜索，再次取中间元素与目标值进行比较，并重复此过程，直到找到目标值。如果搜索结束时剩余部分为空，则目标值不在数组中。尽管这个想法很简单，但正确实现二分查找需要关注一些关于其退出条件和中点计算的细微之处，特别是如果数组中的值并非该范围内所有整数时。
二分查找是最流行的搜索算法。它效率高，也是解决问题的最常用技术之一。
如果将世界上所有姓名按顺序排列在一起，并且您想搜索特定姓名的位置，则二分查找最多可在35次迭代中完成此操作。
二分查找仅适用于已排序的元素集合。要在集合上使用二分查找，必须先对集合进行排序。
当使用二分查找对已排序集合执行操作时，可以根据被搜索的值始终减少迭代次数。
让我们考虑以下数组：
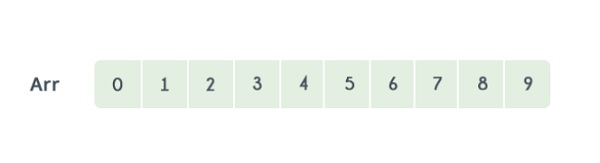
使用线性搜索，将在第9次迭代中确定元素8的位置。
让我们看看如何使用二分查找减少迭代次数。在开始搜索之前，我们需要知道范围的起始位置和结束位置。我们称它们为Low和High。
Low = 0 High = n-1
现在，将搜索值K与位于下界和上界中位数的元素进行比较。如果值K更大，则增加下界，否则减少上界。
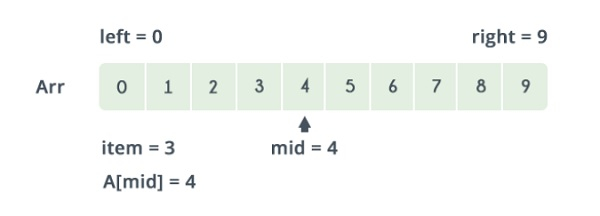
参考上图，下界为0，上界为9。
下界和上界的中间值是 (lower_bound + upper_bound) / 2 = 4。这里 a[4] = 4。值 4 > 2，这就是您要搜索的值。因此，我们不需要对超过4的任何元素进行搜索，因为超过4的元素显然大于2。
因此，我们始终可以将数组的上界降低到元素4的位置。现在，我们在同一个数组上使用以下值遵循相同的过程：
Low: 0 High: 3
递归地重复此过程，直到 Low > High。如果在任何迭代中，我们得到 a[mid] = key，则返回 mid 的值。这是 key 在数组中的位置。如果 key 不存在于数组中，则返回 -1。
示例
int binarySearch(int low,int high,int key){
while(low<=high){
int mid=(low+high)/2;
if(a[mid]<key){
low=mid+1;
}
else if(a[mid]>key){
high=mid-1;
}
else{
return mid;
}
}
return -1; //key not found
}
778 次浏览
