数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++ 中的二叉搜索树 - 搜索和插入操作
二叉搜索树 (BST) 是一种特殊的树，遵循以下规则：
- 左子节点的值始终小于父节点
- 右子节点的值始终大于父节点。
- 所有节点单独构成一个二叉搜索树。
二叉搜索树 (BST) 示例：
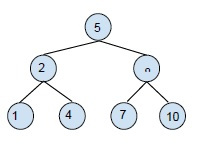
创建二叉搜索树是为了降低搜索、查找最小值和最大值等操作的复杂度。
BST 中的搜索操作
在二叉搜索树中执行搜索：
我们需要在树中搜索一个键。为此，我们将键与树的根节点进行比较。
如果键等于根节点，则找到键。
如果键的值大于根节点，则取右子树并搜索键。
如果键的值小于根节点，则取左子树并搜索键。
示例
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void traversetree(struct node *root){
if (root != NULL){
traversetree(root->left);
printf("%d \t", root->key);
traversetree(root->right);
}
}
struct node* search(struct node* root, int key){
if (root == NULL || root->key == key)
return root;
if (root->key < key)
return search(root->right, key);
return search(root->left, key);
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 23);
insert(root, 15);
insert(root, 12);
insert(root, 17);
insert(root, 32);
insert(root, 29);
insert(root, 45);
printf("The tree is :\n");
traversetree(root);
printf("\nSearching for 12 in this tree ");
if(search(root , 12))
printf("\nelement found");
else
printf("\nelement not found");
return 0;
}输出
The tree is : 12 15 17 23 29 32 45 Searching for 12 in this tree element found
BST 中的插入操作
BST 中的插入操作发生在树的叶节点处。对于插入，我们将开始将节点与根节点进行比较，并找到节点的正确位置，然后将其放置。下面的示例将使您更加清楚。
将 12 插入此 BST。
我们将 12 与根节点进行比较：12 > 5，它属于右子树。
将 12 与右子节点进行比较：12 > 8，它属于右子树的右侧。
将 12 与右子树的右子节点进行比较：12 > 10，它的位置在这个节点的右侧。
形成的新树将是：
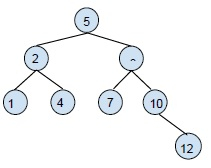
示例
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void traversetree(struct node *root){
if (root != NULL){
traversetree(root->left);
printf("%d \t", root->key);
traversetree(root->right);
}
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 23);
insert(root, 15);
insert(root, 12);
insert(root, 17);
insert(root, 32);
insert(root, 29);
printf("The tree is :\n");
traversetree(root);
printf("\nInseting 45 to the tree\n");
insert(root, 45);
printf("Tree after insertion is :\n");
traversetree(root);
return 0;
}输出
The tree is : 12 15 17 23 29 32 Inserting 45 to the tree Tree after insertion is : 12 15 17 23 29 32 45
更新于：2020年1月3日
2K+ 次浏览
广告