广度优先搜索是机器学习中统一代价搜索的一种特殊情况

在本文中，我们将学习广度优先搜索是如何成为机器学习中统一代价搜索的一种特定情况的。无论是谁在执行（人类或人工智能），他们都必须考虑从改变初始状态到目标状态（如果存在）可能产生的所有场景，以及所有可以想象的结果。人工智能系统也是如此，它们根据所需状态（如果存在）采用各种搜索方法。

什么是广度优先搜索？

它是一种人工智能搜索方法，它以广度优先的方式探索树以找到目标。最常见的方法是广度优先搜索算法（BFS）。BFS 是一种图遍历技术，您从源节点开始，并遍历图，研究与源节点紧密相关的节点。然后，在 BFS 遍历中，您必须转到下一级的邻居节点。

根据 BFS，您必须以广度优先的方向探索图 -

  • 首先水平移动并访问当前层中的所有节点。
  • 继续到下一层。

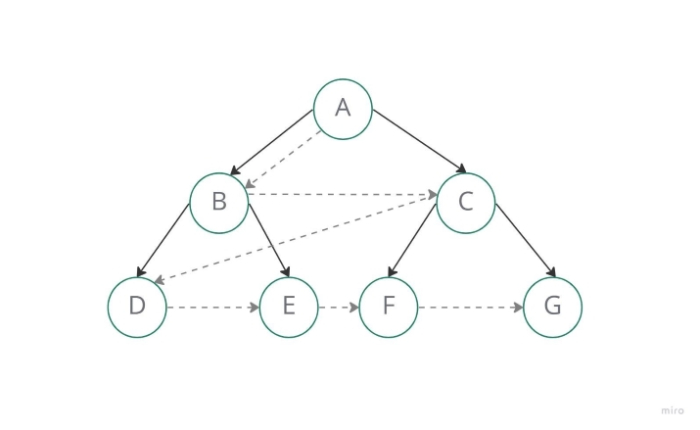
在执行广度优先搜索时，使用队列数据结构来存储节点并在其标记了所有与其直接连接的相邻顶点后将其标记为“已访问”。根据先进先出（FIFO）原则，队列按添加节点的顺序查看每个节点的邻居，从第一个放置的节点开始。

优点

  • 只要有解决方案可用，BFS 就会提供它。

  • 如果某个问题有多个解决方案，BFS 将提供步骤最少且成本最低的解决方案。

缺点

  • 由于必须在扩展到下一层之前将树的每一层都存储在内存中，因此需要大量的内存。

  • 如果答案位于远离根节点的位置，则 BFS 需要大量时间。

伪代码

Bredth_First_Serach( G, A ) // G is the graph, and A is the source node
Let q be the queue
q.enqueue( A ) // Inserting source node A to the queue
Mark A node as visited.
While ( q is not empty )
B = q.dequeue( ) // Removing that vertex from the queue, which will be
visited by its neighbour
Processing all the neighbours of B
For all neighbours of C of B
C is not visited, q. enqueue( C ) //Stores C in q to visit its neighbour
Mark C a visited

什么是统一代价搜索？

当步骤成本不同但必须以最佳方式解决目标状态时，通常会使用此方法。当这种情况发生时，我们使用统一代价搜索来识别目标以及路径，其中包括从根节点到目标节点扩展每个节点所产生的总成本。它不会深度或广度搜索；相反，它寻找具有最低成本的下一个节点。在成本相同的路径的情况下，让我们考虑词典顺序。

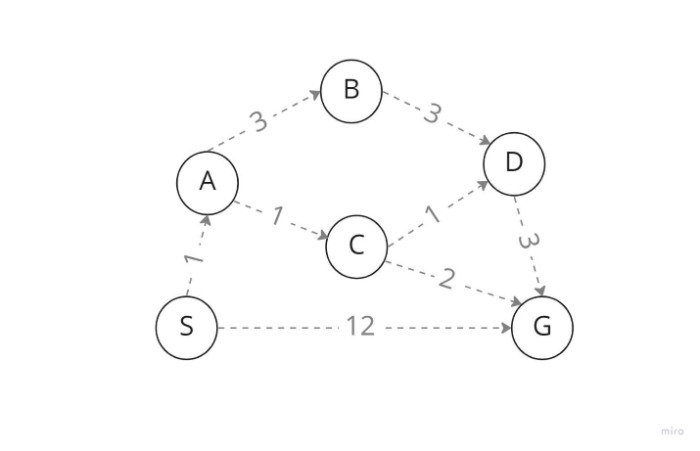
在上图中，将 S 视为起始节点，将 G 视为目标状态。我们搜索要从节点 S 扩展的节点，我们的选择是节点 A 和 G。但是，因为这是统一代价搜索，所以它扩展了具有最低步骤成本的节点，使节点 A 成为后继节点而不是我们需要的目标节点 G。我们从 A 检查 B 和 C，A 的子节点。因此，由于节点 C 具有最低的步骤成本，因此它通过节点 C 遍历。然后，由于节点 D 和 G 是 C 的后继节点并且具有较低的步骤成本，因此我们也使用 D 进行扩展。

最后，通过使用 UFS 算法，我们获得了目标状态 D，因为 D 只有一个子节点 G，这是我们需要的有条件的目标状态。如果我们走过这条路线，我们的总路径成本从 S 到 G 只有 6，即使经过多个节点（就步骤成本而言），而不是直接到达 G，其中成本为 12 且 6<<12。但并非每种情况都适合这种情况。

优点

  • 在每个状态下选择成本最低的路径，使统一代价搜索成为最佳选择。

缺点

  • 它主要关注路径成本，而不考虑搜索过程中涉及多少步骤。因此，此算法可能会陷入无限循环。

伪代码

function UCS(Graph, start, target):
   Add the starting node to the opened list. The node has
   has zero distance value from itself
   while True:
      if opened is empty:
         break # No solution found
      selecte_node = remove from opened list, the node with
         the minimun distance value
      if selected_node == target:
         calculate path
         return path
      add selected_node to closed list
      new_nodes = get the children of selected_node
      if the selected node has children:
         for each child in children:
            calculate the distance value of child
            if child not in closed and opened lists:
               child.parent = selected_node
               add the child to opened list
      else if child in opened list:
         if the distance value of child is lower than 
            the corresponding node in opened list:
               child.parent = selected_node
               add the child to opened list

从广度优先搜索驱动统一代价搜索

UCS 通过添加三个更改来增强广度优先搜索。

首先，它使用优先级队列作为其边界。它根据 g（从起始节点到边界节点的路径成本）对边界节点进行排序。在选择节点进行扩展时，UCS 从边界中选择 g 值最小的节点，即成本最低的节点。

但是，仅仅因为我们将节点添加到边界并不意味着我们知道到节点状态的最佳路径成本。如果我们扩展节点 v 并发现从 v 到其邻居 u 的路径比 g(w) 成本更低，其中 w 是表示与 u 相同状态的边界节点，我们应该从边界中删除 w 并用 u 替换它。第二个变化是队列更新步骤。

第三个是在我们扩展节点后执行目标测试，而不是在我们将其放入边界时执行。如果我们在将节点放入队列之前对其进行验证，我们可能会返回到目标的次优路径。为什么？因为 UCS 能够在其执行的后期识别出更好的路径。

考虑以下广度优先搜索返回的次优路径示例。如果我们在扩展 Start 后立即停止搜索并看到目标节点 Goal 是其邻居，我们将错过经过 A 的理想路径。

结论

用于搜索的无信息搜索技术是一种多功能策略，它结合了无引导搜索的能力和蛮力。由于它们缺乏有关状态空间和目标问题的知识，因此此技术的算法可用于解决各种计算机科学问题。

更新于：2022 年 10 月 28 日

2K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

开始
广告