数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究Go 语言广度优先搜索图
图是一种数据结构，它由边或节点和顶点组成。顶点是节点之间的连线。为了遍历所有这些节点，我们有不同的遍历算法。在本文中，我们将讨论广度优先搜索，或者我们可以称之为 BFS。在广度优先搜索中，我们首先从一个节点开始，然后移动到另一个节点，直到到达死胡同。
示例
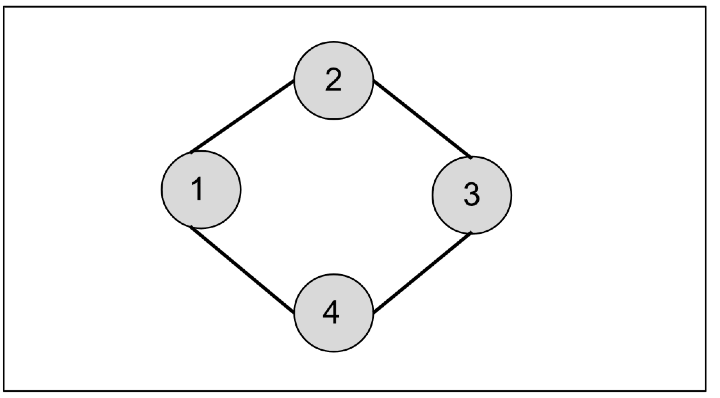
如果我们从节点 1 开始，它将首先访问节点 2 和节点 4。然后从节点 2，我们将访问节点 3。这样，广度优先搜索遍历将是 1、2、4 和 3。
算法
步骤 1：使用 import 关键字在顶部导入所需的包。
步骤 2：然后 main 函数将首先运行。
首先，我们声明并初始化图。
然后我们调用 BFS() 函数，并将图和节点作为参数。
步骤 3：在 BFS() 函数中，以下步骤将在每次函数调用时运行。
isvisited := make(map[int]bool)
创建一个 map，用于存储有关节点是否被访问的信息。
var bfsQueue Queue
为队列数据结构创建一个参数。
isvisited[node] = true, bfsQueue.Enqueue(node)
将传入的节点标记为已访问，并将该节点添加到队列中。
对所有连接的节点运行 for 循环，并将其添加到队列中。
示例 1
在本例中，我们以矩阵的形式表示图，并在矩阵上应用广度优先搜索。这种方法的复杂度将为 O(e*e)，其中 e 是边的数量，空间复杂度为 O(e*e)，即矩阵的大小。
package main
import "fmt"
type Queue struct {
List []int
}
// function to add element in queue
func (q *Queue) Enqueue(element int) {
q.List = append(q.List, element)
}
// function to delete element in the queue
func (q *Queue) Dequeue() int {
if q.isEmpty() {
fmt.Println("Queue is empty.")
return 0
}
element := q.List[0]
q.List = q.List[1:]
return element
}
// function check that queue is empty or not
func (q *Queue) isEmpty() bool {
return len(q.List) == 0
}
// BFS() is a function with matrix and int value as parameter
func BFS(graph [][]int, node int) {
// initializing the map that will keep
// the track is the node is visited or not
isvisited := make(map[int]bool)
// creating a Queue variable
// in which we will add an element at the same level
// of that node
var bfsQueue Queue
// marking current node as visited
isvisited[node] = true
// adding a current node in the queue
bfsQueue.Enqueue(node)
// running a for loop until the queue becomes empty
for !bfsQueue.isEmpty() {
currNode := bfsQueue.List[0]
fmt.Print(currNode, " ")
// adding all the connected node in queue if not visted
for nodes := 0; nodes < len(graph[currNode]); nodes++ {
if graph[currNode][nodes] == 1 && !isvisited[nodes] {
bfsQueue.Enqueue(nodes)
isvisited[nodes] = true
}
}
// removing the current node from queue
// after visiting
bfsQueue.Dequeue()
}
}
func main() {
// matrix representation of the undirected connected graph
// where if the value is 1 the node i is connected
// with node j
graph := [][]int{{0, 1, 0, 1}, {1, 0, 1, 0}, {0, 1, 0, 1}, {1, 0, 1, 0}}
fmt.Println("Golang program to do Breath first search of an undirected connected graph represented in the form of a matrix.")
// calling BFS() function for the breadth-first search
// traversal of a graph
BFS(graph, 0)
fmt.Println()
}
输出
Golang program to do Breath first search of an undirected connected graph represented in the form of a matrix. 0 1 3 2
示例 2
在本例中，我们以邻接表的形式表示图，并相应地应用广度优先搜索。这种方法的复杂度将为 O(e*v)，其中 e 是边的数量，v 是顶点的数量。空间复杂度为 O(e*v)，即邻接表的大小。
package main
import "fmt"
type Queue struct {
List []int
}
// function to add an element in the queue
func (q *Queue) Enqueue(element int) {
q.List = append(q.List, element)
}
// function to delete elements in the queue
func (q *Queue) Dequeue() int {
if q.isEmpty() {
fmt.Println("Queue is empty.")
return 0
}
element := q.List[0]
q.List = q.List[1:]
return element
}
// function checks whether the queue is empty or not
func (q *Queue) isEmpty() bool {
return len(q.List) == 0
}
// BFS() is a function with matrix and int value as parameter
func BFS(graph [4][]int, node int) {
//Initializing the map that will keep
// the track is the node is visited or not
isvisited := make(map[int]bool)
// creating a Queue variable
// in which we will add elements at the same level
// of that node
var bfsQueue Queue
// marking current node as visited
isvisited[node] = true
// adding the current node in the queue
bfsQueue.Enqueue(node)
// running a for loop until the queue becomes empty
for !bfsQueue.isEmpty() {
currNode := bfsQueue.List[0]
fmt.Print(currNode, " ")
// adding all the connected nodes in the queue if not visited
for _, nodes := range graph[currNode] {
if !isvisited[nodes] {
bfsQueue.Enqueue(nodes)
isvisited[nodes] = true
}
}
// removing the current node from queue
// after visiting
bfsQueue.Dequeue()
}
}
func main() {
//adjacency list representation of the undirected connected graph
// where if the value is 1 the node i is connected
// with node j
var graph [4][]int
// initializing each list of the array
graph[0] = []int{1, 3}
graph[1] = []int{0, 2}
graph[2] = []int{1, 3}
graph[3] = []int{0, 2}
fmt.Println("Golang program to do Breath first search of an undirected connected graph represented in the form of an adjacency list.")
// calling BFS() function for the breadth-first search
// traversal of a graph
BFS(graph, 0)
fmt.Println()
}
输出
Golang program to do Breath first search of an undirected connected graph represented in the form of an adjacency list. 0 1 3 2
结论
这两种表示图数据结构和运行广度优先搜索算法的不同方法。第二种方法，我们创建邻接表，在时间和空间上都更有效，因为我们将那些与节点连接的节点号添加到数组中。要了解更多关于 Go 语言的信息，您可以浏览这些 教程。
更新于: 2023年7月10日
1K+ 浏览量
广告