Caffe2 - 创建你自己的网络

上一页
下一页

在本课中，你将学习如何在 Caffe2 中定义一个单层神经网络 (NN)，并在随机生成的数据集上运行它。我们将编写代码来图形化地描绘网络架构，打印输入、输出、权重和偏差值。为了理解本课，你必须熟悉神经网络架构、其术语和其中使用的数学。

网络架构

让我们假设我们想构建一个如下图所示的单层神经网络：

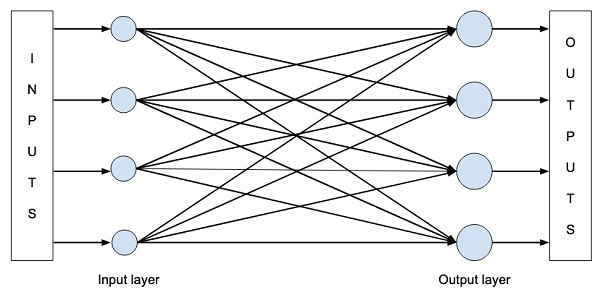
Network Architecture

从数学上讲，这个网络由以下 Python 代码表示：

Y = X * W^T + b

其中X，W，b是张量，Y是输出。我们将用一些随机数据填充所有三个张量，运行网络并检查Y输出。为了定义网络和张量，Caffe2 提供了几个算子函数。

Caffe2 算子

在 Caffe2 中，算子是计算的基本单元。Caffe2 算子表示如下。

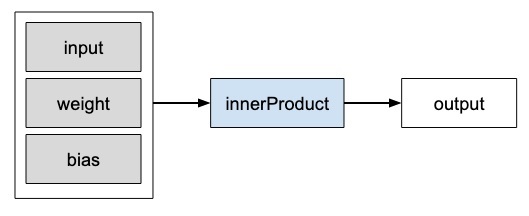
Caffe2 Operators

Caffe2 提供了详尽的算子列表。对于我们目前正在设计的网络，我们将使用称为 FC 的算子，它计算将输入向量X传递到具有二维权重矩阵W和一维偏差向量b的全连接网络的结果。换句话说，它计算以下数学方程

Y = X * W^T + b

其中X的维度为(M x k)，W的维度为(n x k)，b为(1 x n)。输出Y的维度将为(M x n)，其中M是批量大小。

对于向量X和W，我们将使用GaussianFill算子来创建一些随机数据。为了生成偏差值b，我们将使用ConstantFill算子。

我们现在将继续定义我们的网络。

创建网络

首先，导入所需的包：

from caffe2.python import core, workspace

接下来，通过调用core.Net来定义网络，如下所示：

net = core.Net("SingleLayerFC")

网络的名称指定为SingleLayerFC。此时，名为 net 的网络对象被创建。到目前为止，它不包含任何层。

创建张量

我们现在将创建网络所需的三个向量。首先，我们将通过调用GaussianFill算子来创建 X 张量，如下所示：

X = net.GaussianFill([], ["X"], mean=0.0, std=1.0, shape=[2, 3], run_once=0)

X向量的维度为2 x 3，平均数据值为 0.0，标准差为1.0。

同样，我们创建W张量，如下所示：

W = net.GaussianFill([], ["W"], mean=0.0, std=1.0, shape=[5, 3], run_once=0)

W向量的尺寸为5 x 3。

最后，我们创建大小为 5 的偏差b矩阵。

b = net.ConstantFill([], ["b"], shape=[5,], value=1.0, run_once=0)

现在，代码中最重要的部分来了，那就是定义网络本身。

定义网络

我们在以下 Python 语句中定义网络：

Y = X.FC([W, b], ["Y"])

我们在输入数据X上调用FC算子。权重在W中指定，偏差在 b 中指定。输出是Y。或者，你可以使用以下更详细的 Python 语句创建网络。

Y = net.FC([X, W, b], ["Y"])

此时，网络只是被创建了。在我们至少运行一次网络之前，它不包含任何数据。在运行网络之前，我们将检查其架构。

打印网络架构

Caffe2 在 JSON 文件中定义网络架构，可以通过在创建的net对象上调用 Proto 方法来检查。

print (net.Proto())

这将产生以下输出：

name: "SingleLayerFC"
op {
   output: "X"
   name: ""
   type: "GaussianFill"
   arg {
      name: "mean"
      f: 0.0
   }
   arg {
      name: "std"
      f: 1.0
   }
   arg {
      name: "shape"
      ints: 2
      ints: 3
   }
   arg {
      name: "run_once"
      i: 0
   }
}
op {
   output: "W"
   name: ""
   type: "GaussianFill"
   arg {
      name: "mean"
      f: 0.0
   }
   arg {
      name: "std"
      f: 1.0
   }
   arg {
      name: "shape"
      ints: 5
      ints: 3
   }
   arg {
      name: "run_once"
      i: 0
   }
}
op {
   output: "b"
   name: ""
   type: "ConstantFill"
   arg {
      name: "shape"
      ints: 5
   }
   arg {
      name: "value"
      f: 1.0
   }
   arg {
      name: "run_once"
      i: 0
   }
}
op {
   input: "X"
   input: "W"
   input: "b"
   output: "Y"
   name: ""
   type: "FC"
}

正如你在上面的列表中看到的，它首先定义了算子X，W和b。让我们以W的定义为例进行检查。W的类型指定为GausianFill。均值定义为浮点数0.0，标准差定义为浮点数1.0，形状为5 x 3。

op {
   output: "W"
   name: "" type: "GaussianFill"
   arg {
      name: "mean" 
	   f: 0.0
   }
   arg { 
      name: "std" 
      f: 1.0
   }
   arg { 
      name: "shape" 
      ints: 5 
      ints: 3
   }
   ...
}

检查X和b的定义以加深你的理解。最后，让我们看看我们单层网络的定义，这里将其复制如下

op {
   input: "X"
   input: "W"
   input: "b"
   output: "Y"
   name: ""
   type: "FC"
}

在这里，网络类型为FC（全连接），输入为X，W，b，输出为Y。这种网络定义过于冗长，对于大型网络，检查其内容将变得乏味。幸运的是，Caffe2 为创建的网络提供了图形表示。

网络图形表示

要获得网络的图形表示，请运行以下代码片段，它实际上只有两行 Python 代码。

from caffe2.python import net_drawer
from IPython import display
graph = net_drawer.GetPydotGraph(net, rankdir="LR")
display.Image(graph.create_png(), width=800)

运行代码时，你会看到以下输出：

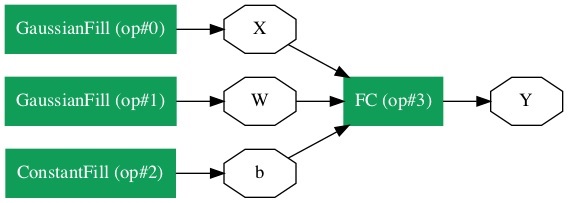
Graphical Representation

对于大型网络，图形表示在可视化和调试网络定义错误方面变得非常有用。

最后，现在是运行网络的时候了。

运行网络

你可以通过在workspace对象上调用RunNetOnce方法来运行网络：

workspace.RunNetOnce(net)

网络运行一次后，我们随机生成的所有数据都将被创建，输入网络，并创建输出。运行网络后创建的张量在 Caffe2 中称为blobs。工作区包含你创建并存储在内存中的blobs。这与 Matlab 非常相似。

运行网络后，你可以使用以下print命令检查工作区包含的blobs

print("Blobs in the workspace: {}".format(workspace.Blobs()))

你会看到以下输出：

Blobs in the workspace: ['W', 'X', 'Y', 'b']

请注意，工作区包含三个输入 blobs——X，W和b。它还包含名为Y的输出 blob。现在让我们检查这些 blobs 的内容。

for name in workspace.Blobs():
   print("{}:\n{}".format(name, workspace.FetchBlob(name)))

你会看到以下输出：

W:
[[ 1.0426593 0.15479846 0.25635982]
[-2.2461145 1.4581774 0.16827184]
[-0.12009818 0.30771437 0.00791338]
[ 1.2274994 -0.903331 -0.68799865]
[ 0.30834186 -0.53060573 0.88776857]]
X:
[[ 1.6588869e+00 1.5279824e+00 1.1889904e+00]
[ 6.7048723e-01 -9.7490678e-04 2.5114202e-01]]
Y:
[[ 3.2709925 -0.297907 1.2803618 0.837985 1.7562964]
[ 1.7633215 -0.4651525 0.9211631 1.6511179 1.4302125]]
b:
[1. 1. 1. 1. 1.]

请注意，你机器上的数据，或者事实上网络的每次运行的数据都会有所不同，因为所有输入都是随机创建的。你现在已成功定义了一个网络并在你的计算机上运行它。

打印页面
上一页
下一页
广告