数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会研究
时尚研究
法律研究在 C++ 中计算置乱数（不出现元素的原位排列）
置乱数是指 N 个数字的排列，使得没有数字出现在其原始位置处。例如，{ 1,2,3 } 可能出现的置乱数为 { 2,1,3 }。其中没有一个元素在原始位置处。我们的目的是计算 N 个数字可能出现的置乱数。
我们将使用递归解法。对于以下元素数 −
- N=0，无置乱数，返回 1
- N=1，只有一个数字，返回 0
- N=2，只可能进行一次位置交换，{ 1,2 } → { 2,1 }，返回 1
- N=3，2 种可能的置乱数，如 { 1,2,3 } → { 2,3,1 }，{ 3,1,2 }，计数 2
- N=4，9 种可能的置乱数
- .......................
- N，(N-1)*( permutation(N-1) + permutation(N-2) )
对于数组中的所有元素来说，
位于索引 0 处的元素有 n-1 个可能的位置，
如果索引 i 处的任何元素位于索引 0 处，则 arr[i] 和 arr[0] 被交换。现在还有 n-2 个元素需要计算。
如果索引 i 处的元素没有位于索引 0 处，则对于 n-1 个元素来说，有 n-2 种选择。
图表
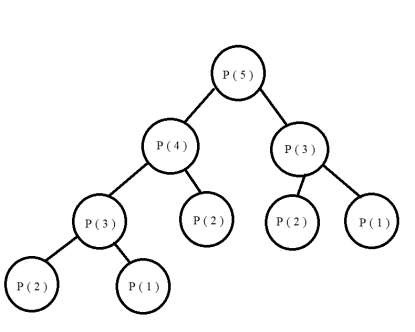
输入
Arr[] = { 1, 2 }输出
No. of derangements : 1
解释 - 位置 1 和 2 的索引为 0 和 1。它们能取得的唯一位置是互换原来的位置。{ 2,1 }
输入
Arr[] = { 1, 2, 3 }输出
No. of derangements : 2
解释 - 位置 1、2 和 3 的索引为 0、1、2。
1 可以放置在索引 1 和 2，2 可以放置在索引 0 和 3，3 可以放置在索引 0 和 1。
{ 2,3,1 } 和 { 3,1,2 } 是 2 个错位排列。
在以下程序中，采用的方法如下
整数 Num 存储存在数字的数量。
递归函数 derangements(int N) 以数字数量作为输入并返回错位排列的数量。
N=0,1,2 的 return 语句处理基准案例，其中排列已计算为 1、0 和 1。
如果 N>2，则使用以下公式对 derangements() 进行递归调用：
(N-1)* ( derangements ( N-1) + derangements ( N-2) )。
当开始回溯时，计算并返回数量。
示例
#include <bits/stdc++.h>
using namespace std;
int derangements(int N){
if (N == 0)
return 1;
if (N == 1)
return 0;
if (N == 2)
return 1;
return (N - 1) * (derangements(N - 1) + derangements(N - 2));
}
int main(){
int Numbers=5;
cout<<"Number of Derangements :"<<derangements(Numbers);
}输出
Number of Derangements :44
更新于: 03-8-2020
538 浏览量
广告