数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究使用 C++ 统计遍历矩阵的方式数量
给定一个维度为行 X 列的二维矩阵。目标是统计从单元格 0,0 到单元格行,列遍历矩阵的方式数量，只能使用向右和向下的移动，即第一步可以从 0,0 移动到 0,1（向下）或 1,0（向右），而不能移动到 1,1（对角线）。
例如
输入
col = 2; row = 4
输出
Count of number of ways to traverse a Matrix are: 4
解释
我们可以从单元格 0,0 到达 2,4 的方式如下所示：
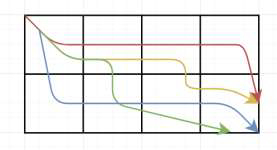
输入
col = 4; row = 3
输出
Count of number of ways to traverse a Matrix are: 10
解释
We will reduce the problem into smaller recursions. Count ways for col=3, row=2, then for col=2, row=1 ….. For col=1 or row=1 the answer will be 1. (only right or only down move).
下面程序中使用的方案如下
在这种方案中，我们将使用递归方法。对于行或列为 1 的情况，只有一种方式，即 1 个向右的直线移动或 1 个向下的直线移动。这将是递归的终止条件。
获取矩阵维度的整数行和列。
函数 ways_traverse_matrix(int row, int col) 获取维度并返回遍历矩阵的方式数量。
如果 row==1，则返回 1。
如果 col==1，则返回 1。
否则，使用递归计算方式 ways_traverse_matrix(temp_1, col) + ways_traverse_matrix(row, temp_2)。
这里 temp_1=上一行号，temp_2=上一列号。
最后，我们将得到总方式的数量。
示例
#include <bits/stdc++.h>
using namespace std;
int ways_traverse_matrix(int row, int col){
if (row == 1){
return 1;
}
else if(col == 1){
return 1;
} else {
int temp_1 = row − 1;
int temp_2 = col − 1;
return ways_traverse_matrix(temp_1, col) + ways_traverse_matrix(row, temp_2);
}
}
int main(){
int col = 2;
int row = 2;
cout<<"Count the number of ways to traverse a Matrix are: "<<ways_traverse_matrix(row, col);
return 0;
}输出
如果我们运行以上代码，它将生成以下输出：
Count the number of ways to traverse a Matrix are: 2
更新于: 2021年1月5日
235 次浏览
广告