数据结构中缓存未命中的计数

在算法分析中，我们计算操作和步骤。当计算机执行操作所需的时间比获取该操作所需数据的时间长得多时，这基本上是合理的。如今，执行操作的成本远低于从内存中获取数据的成本。

许多算法的运行时间主要取决于内存引用次数（缓存未命中次数），而不是操作次数。因此，当我们尝试设计一些算法时，我们必须关注的不仅是减少操作次数，还要减少内存访问次数。还必须专注于设计能够隐藏内存延迟的算法。

假设存在一个简单的计算机模型，其中计算机的内存由L1缓存、L2缓存和主内存组成。我们使用ALU对寄存器(R)中驻留的数据执行一些算术和逻辑运算。

这是它的框图：

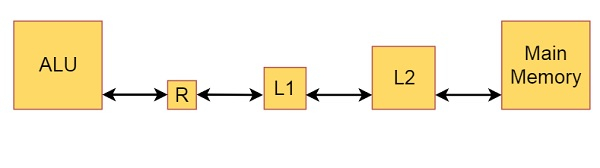
从图中我们还可以了解内存和缓存的大小。主内存基本上是数百或数千MB。L2缓存是MB的一小部分，L1缓存是KB。寄存器大小为几比特。当我们执行程序时，所有数据都在内存中。如果我们添加一些操作，例如ADD，则第一个数字将存储到寄存器中，寄存器中的数据将被添加，然后结果将被写入内存。

假设一个周期是将已在寄存器中的数据相加所需的时间长度。在这个模型中，从L1缓存加载数据到寄存器所需的时间假设为两个周期。如果所需数据不在L1缓存中，但在L2缓存中，则会发生L1缓存未命中，所需数据将从L2缓存取到L1缓存和寄存器中，需要10个周期。当所需数据也不在L2缓存中时，会发生L2缓存未命中，所需数据将从主内存取到L2缓存、L1缓存和寄存器中，需要100个周期。然后，即使数据写入主内存，写入操作也计为一个周期，因为我们不会在继续下一个操作之前等待完成写入。

更新于：2020年8月10日

212 次浏览

启动您的职业生涯

完成课程获得认证

开始学习
广告