数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学C++程序实现给定二叉树的非递归先序遍历
树的遍历是图遍历的一种形式。它涉及到精确地检查或打印树中的每个节点一次。二叉搜索树的先序遍历涉及按（根、左、右）的顺序访问树中的每个节点。
二叉树的先序遍历示例如下。
给定一个二叉树如下所示。
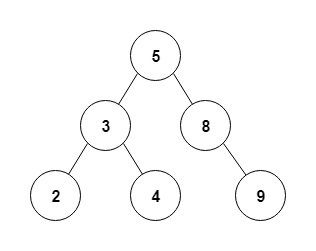
先序遍历结果：5 3 2 4 8 9
下面给出一个执行非递归先序遍历的程序。
示例
#include<iostream>
#include <stack>
using namespace std;
struct node {
int data;
struct node *left;
struct node *right;
};
struct node *createNode(int val) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp→data = val;
temp→left = temp→right = NULL;
return temp;
}
void preorder(struct node *root) {
if (root == NULL)
return;
stack<node *> nodeStack;
nodeStack.push(root);
while (nodeStack.empty() == false) {
struct node *temp_node = nodeStack.top();
cout<< temp_node->data <<" ";
nodeStack.pop();
if (temp_node→right)
nodeStack.push(temp_node->right);
if (temp_node→left)
nodeStack.push(temp_node->left);
}
}
struct node* insertNode(struct node* node, int val) {
if (node == NULL) return createNode(val);
if (val < node→data)
node→left = insertNode(node→left, val);
else if (val > node→data)
node→right = insertNode(node→right, val);
return node;
}
int main() {
struct node *root = NULL;
root = insertNode(root, 5);
insertNode(root, 8);
insertNode(root, 3);
insertNode(root, 2);
insertNode(root, 6);
insertNode(root, 9);
insertNode(root, 4);
cout<<"Pre-Order traversal of the Binary Search Tree is: ";
preorder(root);
}输出
Pre-Order traversal of the Binary Search Tree is: 5 3 2 4 8 6 9
在上面的程序中，结构体node创建树的节点。这个结构体是一个自引用结构体，因为它包含struct node类型的指针。该结构体如下所示。
struct node {
int data;
struct node *left;
struct node *right;
};createNode()函数创建一个节点temp并使用malloc为其分配内存。数据值val存储在temp的数据中。NULL存储在temp的左和右指针中。这可以通过以下代码片段演示。
struct node *createNode(int val) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp→data = val;
temp→left = temp→right = NULL;
return temp;
}preorder()函数使用堆栈以先序打印树的元素。首先将根节点插入堆栈。启动一个while循环，直到堆栈不为空。首先显示堆栈顶部元素topnode中的数据，然后弹出该节点。然后将上述节点的右节点和左节点压入堆栈。
此函数使用以下代码片段进行演示。
void preorder(struct node *root) {
if (root == NULL)
return;
stack<node *> nodeStack;
nodeStack.push(root);
while (nodeStack.empty() == false) {
struct node *temp_node = nodeStack.top();
cout<< temp_node->data <<" ";
nodeStack.pop();
if (temp_node→right)
nodeStack.push(temp_node→right);
if (temp_node→left)
nodeStack.push(temp_node→left);
}
}insertNode()函数将所需的值插入到二叉树的正确位置。如果节点为NULL，则调用createNode。否则，在树中找到节点的正确位置。这可以在下面的代码片段中观察到。
struct node* insertNode(struct node* node, int val) {
if (node == NULL) return createNode(val);
if (val < node→data)
node→left = insertNode(node→left, val);
else if (val > node→data)
node->right = insertNode(node→right, val);
return node;
}在main()函数中，首先将根节点定义为NULL。然后将所有具有所需值的节点插入到二叉搜索树中。如下所示。
struct node *root = NULL; root = insertNode(root, 5); insertNode(root, 8); insertNode(root, 3); insertNode(root, 2); insertNode(root, 6); insertNode(root, 9); insertNode(root, 4);
最后，使用树的根节点调用preorder()函数，并以先序显示所有树的值。如下所示。
cout<<"Pre-Order traversal of the Binary Search Tree is: "; preorder(root);
更新于：2020年6月24日
浏览量1K+
广告