简并轨道

---

简介

简并轨道是指同一亚层中具有相同能级的电子轨道。如果磁场不干扰这些轨道，则简并轨道始终存在。简并性会干扰磁场的应用方式。

通过可视化学习物质和化合物的知识是化学课程的关键组成部分。在这里，我们将通过理解简并轨道的含义以及 Aufbau 原理和 Hund 规则的相关概念，来学习原子的基本结构。

Hund 最大多重性规则

• 根据 Hund 最大多重性规则，对于特定的电子构型，具有最大多重性的项具有最低的能量。根据该规则，p、d 和 f 轨道中的电子只有在每个轨道中都存在一个电子或完全填充时才会配对。

• 电子填充简并轨道。

• 根据弗里德里希·洪特的 Hund 多重性定律，在亚层中，每个轨道先填充一个电子，然后再向任何轨道填充第二个电子。

• 电子始终以相同的自旋量子数填充亚层，直到每个轨道中至少有一个电子。

• 在特定电子构型中，Hund 的多重性规则指出，在 f、p 和 d 轨道中，电子配对永远不会发生，直到亚层中的每个轨道都填充了一个电子。假设一个碳原子具有电子构型 1𝑠22𝑠22𝑝2。根据 Hund 规则，2 个 2s 电子将填充该轨道，而 2 个 2p 电子将填充其他每个轨道。

什么是 Hund 规则？

根据 Hund 的电子规则，简并轨道会均匀地被占据，然后再占据较高能级的电子。Aufbau 原理、泡利不相容原理和 Hund 规则是解释电子在后续能级中填充的三个概念。

Hund 规则的假设

• 根据该规则，在亚层中，一个轨道先被填充，然后再被另一个轨道占据。

• 在各个轨道中的电子的自旋与跨多个轨道的电子的自旋相同。

Hund 规则的描述

当电子接近轨道时，它们彼此配对。这些带负电的原子彼此排斥。由于它们不共享轨道，因此电子之间的排斥力较小。

当我们分析第二条规则时，单独填充的轨道中未配对电子的自旋是相同的。该能级上第一个电子的自旋决定了亚层中所有其他电子的自旋。这在 𝐶 原子的电子构型（为 1𝑠22𝑠22𝑝2）中是一个例子。根据 Hund 规则，2 个 2s 电子将占据相同的轨道，但 2 个 2p 电子将占据不同的轨道。

什么是 Aufbau 原理？

根据 Aufbau 原理，电子从较低能级开始，按照从低到高的顺序填充能级。电子以递增的 n+l 值填充，其中 n 是主量子数，l 是角量子数。这个概念有助于预测原子可能形成的化学键类型。

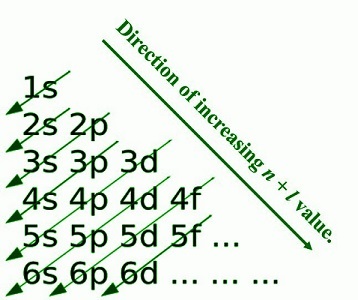
Goodphy，Madelung 规则图，CC BY-SA 4.0

简并轨道示例

这是一个简并轨道的示例。

示例 - s、p、d 和 f 是构成原子的 4 个轨道。p 轨道中有 3 个轨道：𝑝𝑥、𝑝𝑦 和 𝑝𝑧。由于这 3 个轨道的能量相同并且对应于相同的轨道 (p)，因此它们被称为简并分子轨道。每个轨道先填充一个电子，然后是具有相反自旋的下一个电子填充相同的轨道。最终，p 轨道被占据，3 个轨道各包含 6 个电子。

使用图表解释简并轨道

为了可视化这个概念，让我们通过使用图表对简并轨道进行详细的解释。2p 轨道的电子填充过程需要 2𝑝𝑥、2𝑝𝑦 和 2𝑝𝑧。这些轨道彼此之间具有相同的能量。3p 轨道的电子填充过程也包括 3𝑝𝑥、3𝑝𝑦 和 3𝑝𝑧。简并分子轨道是指具有相同能级的轨道。由于 4p 中的 4𝑝𝑥、4𝑝𝑦 和 4𝑝𝑧 电子彼此之间具有相同的能级，因此它们也是简并的。现在让我们使用图形表示来评估这些能量亚层简并性。

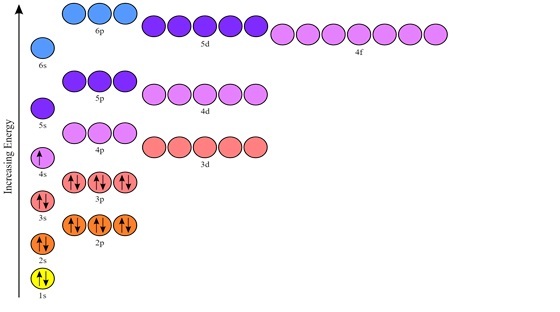
CK-12 基金会，钾的轨道表示图，CC BY-SA 3.0

结论

可以得出结论，简并轨道是具有相同能级的电子轨道。任何外部影响（例如电场/磁场）都不会影响轨道的电子。这些轨道的简并性会干扰磁场的应用。具有相同能量的是简并轨道。轨道填充的原子是最稳定的原子，并且不会与其他元素相互作用。根据弗里德里希·洪特，在基态电子构型中，任何亚层中的大多数电子自旋都是平行的。Aufbau 原则预测电子将占据从低到高的能级。p、d 和 f 轨道的简并度值分别为 3、5 和 7。

常见问题

1. 当 3d 轨道被填充时，下一个电子将进入哪里？

如 Aufbau 原理所述，电子将从较低能级跃迁到较高能级。电子将进入 4p 轨道，因为它比 3d 轨道具有更高的能级。

2. 什么导致简并？

泡利不相容原理禁止粒子在彼此非常靠近时具有相同的能量，这会导致粒子相互排斥。由此产生的简并压力与热压力相反，它仅取决于密度，而不取决于温度。

3. Hund 规则在何种简并轨道中失效？

每个具有相同能量的轨道必须先填充一个具有相同自旋的电子，然后才能在同一轨道中填充两个电子，这与 Hund 规则相矛盾。这些电子的排列违反了 Hund 规则。

4. 3d 轨道完全占据后，进入的电子将进入哪个轨道？

根据 Aufbau 原理，当电子到达时，它会从较低能级跃迁到较高能级。如果第三个轨道已满，则电子将进入下一个较高能级轨道，即 4p 轨道。

5. 描述简并特征值？

如果多个线性无关的本征态属于给定的特征值，则该特征值被称为简并。经典和量子力学问题都可能发生简并，它几乎总是与系统的空间对称性相关。