图的顶点度数

---

它是与顶点V相邻的顶点数。

符号 − deg(V)。

在一个具有n个顶点的简单图中，任何顶点的度数为−

deg(v) = n – 1 ∀ v ∈ G

一个顶点可以与除自身以外的所有其他顶点形成边。因此，顶点的度数最多为图中顶点数减1。这个1是自顶点，因为它不能独自形成环。如果任何顶点都有环，则它不是简单图。

顶点的度数可以在图的两种情况下考虑：

• 无向图
• 有向图

无向图中顶点的度数

无向图没有有向边。考虑以下示例。

示例1

看看下面的图：

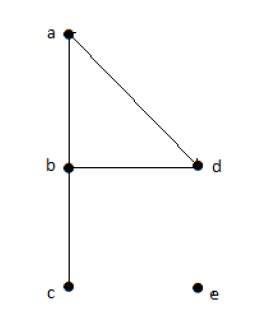
在上图的无向图中，

• deg(a) = 2，因为在顶点'a'处有2条边相交。

• deg(b) = 3，因为在顶点'b'处有3条边相交。

• deg(c) = 1，因为在顶点'c'处形成1条边

  所以'c'是悬挂顶点。

• deg(d) = 2，因为在顶点'd'处有2条边相交。

• deg(e) = 0，因为在顶点'e'处没有形成边。

  所以'e'是孤立顶点。

示例2

看看下面的图：

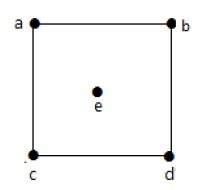
在上图中，

deg(a) = 2, deg(b) = 2, deg(c) = 2, deg(d) = 2, deg(e) = 0。

顶点'e'是孤立顶点。该图没有悬挂顶点。

有向图中顶点的度数

在有向图中，每个顶点都有一个入度和一个出度。

图的入度

• 顶点V的入度是指进入顶点V的边的数量。

• 符号 − deg⁻(V)。

图的出度

• 顶点V的出度是指从顶点V出去的边的数量。

• 符号 − deg⁺(V)。

考虑以下示例。

示例1

看看下面的有向图。顶点'a'有两条边'ad'和'ab'指向外部。因此，它的出度为2。同样，有一条边'ga'指向顶点'a'。因此，'a'的入度为1。

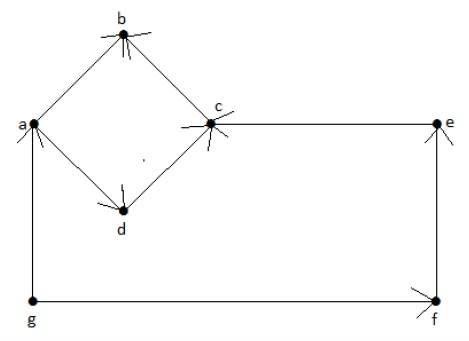
其他顶点的入度和出度如下表所示：

顶点	入度	出度
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

示例2

看看下面的有向图。顶点'a'有一条边'ae'从顶点'a'指向外部。因此，它的出度为1。同样，该图有一条边'ba'指向顶点'a'。因此，'a'的入度为1。

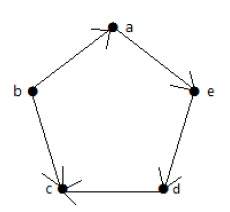
其他顶点的入度和出度如下表所示：

顶点	入度	出度
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1