检测有向图中的环
使用深度优先搜索 (DFS) 遍历算法,我们可以检测有向图中的环。如果任何节点存在自环,则将其视为一个环;否则,当子节点有另一条边连接其父节点时,它也构成一个环。
对于非连通图,可能存在不同的树,我们可以称之为森林。现在我们必须检测森林中所有树的环。
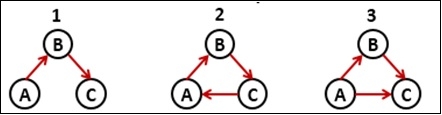
在这种方法中,我们将使用不同的集合来分配节点以执行 DFS 遍历。有三种不同的集合:白色、灰色和黑色。最初,所有节点都将存储在白色集合中。当遍历一个新节点时,它将存储在灰色集合中并从白色集合中移除。并且在完成回溯后,当该节点的任务完成后,它将从灰色集合交换到黑色集合。
输入和输出
Input: The Adjacency matrix. 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 Output: The graph has cycle.
算法
dfs(curr, wSet, gSet, bSet)
输入:当前节点、白色集合、灰色集合和黑色集合。
输出:如果存在环则返回 True。
Begin delete curr from the while set and add it to the grey set for all nodes v connected with curr in the graph, do if v is in the black set, then skip next part, and go for next iteration if v is in the grey set, then return true if dfs(v, wSet, gSet, bSet) is true, then return true done delete curr from grey set and add to black set return fasle End
hasCycle(graph)
输入 - 给定的图。
输出: 当图包含环时返回 True。
Begin initially insert all nodes into the white set while white set has some elements, do for all nodes v in the graph, do if v is not in the white set, then if dfs(v, wSet, gSet, bSet), then return true done done return false End
示例
#include<iostream>
#include<set>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 0, 0, 0},
{0, 0, 0, 0, 0},
{1, 0, 0, 1, 0},
{0, 0, 0, 0, 1},
{0, 0, 1, 0, 0}
};
bool dfs(int curr, set<int>&wSet, set<int>&gSet, set<int>&bSet) {
//moving curr to white set to grey set.
wSet.erase(wSet.find(curr));
gSet.insert(curr);
for(int v = 0; v < NODE; v++) {
if(graph[curr][v] != 0) { //for all neighbour vertices
if(bSet.find(v) != bSet.end())
continue; //if the vertices are in the black set
if(gSet.find(v) != gSet.end())
return true; //it is a cycle
if(dfs(v, wSet, gSet, bSet))
return true; //cycle found
}
}
//moving v to grey set to black set.
gSet.erase(gSet.find(curr));
bSet.insert(curr);
return false;
}
bool hasCycle() {
set<int> wSet, gSet, bSet; //three set as white, grey and black
for(int i = 0; i<NODE; i++)
wSet.insert(i); //initially add all node into the white set
while(wSet.size() > 0) {
for(int current = 0; current < NODE; current++) {
if(wSet.find(current) != wSet.end())
if(dfs(current, wSet, gSet, bSet))
return true;
}
}
return false;
}
int main() {
bool res;
res = hasCycle();
if(res)
cout << "The graph has cycle." << endl;
else
cout << "The graph has no cycle." << endl;
}输出
The graph has cycle.

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP