数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究A*算法和AO*算法的区别
在人工智能和计算机科学领域，搜索算法对于解决具有挑战性的问题至关重要。想象一下，你在一个巨大的迷宫中寻找出口。你可能会无目的地尝试每条路径，希望最终能找到出口。但是，如果有一个熟悉迷宫的向导来帮助你，岂不是更好？在数字领域，搜索算法就像迷宫中的向导！它们帮助计算机像你在迷宫中一样，在众多选项中确定最佳路径。A* 和 AO* 就是两个这样的算法。在这篇博文中，我们将讨论它们的定义、机制以及它们之间的主要区别。
引言
计算机使用专门的算法来找到复杂问题的有效解决方案，例如选择穿过迷宫的最佳路径或在游戏中做出决策。A*（发音为“A-star”）和 AO*（发音为“A-O-star”）是这两种算法的示例。它们都希望找到到达目标的最快路径，但它们采取不同的方法，并且关注不同的问题。
什么是算法？
在我们继续讨论 A* 和 AO* 之前，让我们先构建一个算法。计算机使用一组称为算法的指令来执行任务或解决问题。例如，你用来烘焙蛋糕的食谱就是一个算法。在这个例子中，为了获得期望的结果——一个美味的蛋糕——它指导你完成过程的每一步！
什么是搜索算法？
搜索算法就像解决问题的超级英雄。当主要目标是确定最佳选择并且有多个选项时，它们就会发挥作用。想象一个电脑游戏，你的角色需要到达一个宝箱。可能存在无数条路径，但有些路径可能很清晰，而另一些路径可能包含怪物。为了到达宝箱，搜索算法会评估每条路径，并选择最短和最安全的路径！
关键术语
- 寻路：找到从一点到另一点的最佳路径。
- 图遍历：图遍历是指访问图中的每个节点/点，图是由连接的点组成的网络。
- 启发式：一种智能猜测，用于估计从任何给定节点到达目标的成本。
什么是 A* 算法？
A* 的功能类似于一个非常聪明的寻路者。想象一下，你在迷宫中试图找出最快逃脱的路径。借助 A* 算法，你可以找到这条路径，它会考虑你已经走过的距离以及剩余的距离。它将这两个因素结合起来，在每个阶段确定最佳选择，确保快速有效地完成你的任务。A* 通过将这些成本 (f) 相加来确定最佳行动方案。
f(n) = g(n) + h(n)
- g(n)：从起点到当前节点的实际成本。
- h(n)：从当前节点到目标的估计成本。
A* 如何工作？
A* 使用两条主要信息
- G 值：这是从起点到当前点所花费的成本。
- H 值（启发式）：H 值（启发式）提供从当前位置移动到目标的成本估计。
A* 算法示例
假设你在迷宫中
- G 值是你已经走过的步数。
- H 值是你认为还需要走多少步。
A* 将通过始终选择 G + H 最小的路径来帮助你找到最短路径。
| 步骤 | 已走路径（G 值） | 估计剩余路径（H 值） | 总成本（F 值） |
| 1 | 2 步 | 6 步 | 8 |
| 2 | 3 步 | 4 步 | 7 |
| 3 | 4 步 | 2 步 | 6 |
什么是 AO* 算法？
AO* 算法是另一种解决问题的技术，尽管它仅限于需要决策并将问题分解成可管理部分的任务。AO* 算法是为动态情况设计的 A* 算法的变体。它不必重新开始搜索以适应变化。想象一个机器人穿过一个区域，家具不断移动。假设你必须在解决谜题时在每个转弯处做出决定。借助 AO* 算法，你可以通过确定最佳行动方案组合来更快地解决谜题。
AO* 如何工作？
AO* 稍微复杂一些，因为它处理所谓的 AND-OR 图。这意味着，除了只考虑一种可能的路径（如 A*）之外，该算法还会考虑可能协同解决问题的多种选择。
- AND 节点：这些是必须同时做出多个选择才能继续的点。
- OR 节点：这些是必须从多个选项中选择一个才能继续的点。
AO* 算法将这些选择组合起来以找到问题的最佳解决方案。
AO* 算法示例
可以这样理解
- AND 节点：如果你想烤蛋糕，你需要面粉 AND 糖。
- OR 节点：香草 OR 巧克力是你的蛋糕调味料选择。
AO* 将检查这些组合中的每一个，以查看哪个食谱能做出最美味的蛋糕。
A* 和 AO* 算法之间的主要区别
现在我们已经熟悉了 A* 和 AO* 算法的基本知识，让我们在一个简单的表格中检查它们之间的主要区别
| 特征 | A* 算法 | AO* 算法 |
| 问题类型 | 寻路（找到最短路径） | 决策（找到最佳策略） |
| 图类型 | 简单图 | AND-OR 图 |
| 决策 | 一次考虑一条路径 | 考虑多条路径和组合 |
| 复杂度 | 不太复杂 | 更复杂 |
| 用例 | 迷宫求解、GPS 导航 | 游戏策略、复杂问题解决 |
使用 Python 代码和可视化进行实现
A*（A 星）算法是一种流行的寻路和图遍历算法，用于查找从起始节点到目标节点的最短路径。它结合了 Dijkstra 算法和贪婪最佳优先搜索的优点。使用 Python 代码和可视化来实现 A* 算法
import matplotlib.pyplot as plt
import numpy as np
import heapq
# Define the grid and obstacles
grid_size = (10, 10)
start = (0, 0)
goal = (9, 9)
obstacles = [(4, i) for i in range(4, 7)] + [(i, 4) for i in range(4, 7)]
def heuristic(a, b):
return abs(a[0] - b[0]) + abs(a[1] - b[1])
def a_star(grid_size, start, goal, obstacles):
open_set = []
heapq.heappush(open_set, (0 + heuristic(start, goal), 0, start))
came_from = {}
g_score = {start: 0}
f_score = {start: heuristic(start, goal)}
while open_set:
_, current_g, current = heapq.heappop(open_set)
if current == goal:
path = []
while current in came_from:
path.append(current)
current = came_from[current]
path.append(start)
path.reverse()
return path
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
neighbor = (current[0] + dx, current[1] + dy)
if (0 <= neighbor[0] < grid_size[0] and
0 <= neighbor[1] < grid_size[1] and
neighbor not in obstacles):
tentative_g_score = g_score[current] + 1
if neighbor not in g_score or tentative_g_score < g_score[neighbor]:
came_from[neighbor] = current
g_score[neighbor] = tentative_g_score
f_score[neighbor] = tentative_g_score + heuristic(neighbor, goal)
heapq.heappush(open_set, (f_score[neighbor], tentative_g_score, neighbor))
return []
def plot_path(grid_size, obstacles, path):
grid = np.zeros(grid_size)
for (i, j) in obstacles:
grid[i, j] = -1
for (i, j) in path:
grid[i, j] = 1
plt.imshow(grid, cmap='Greys', interpolation='none')
plt.colorbar()
plt.title("A* Pathfinding")
plt.show()
path = a_star(grid_size, start, goal, obstacles)
plot_path(grid_size, obstacles, path)
输出
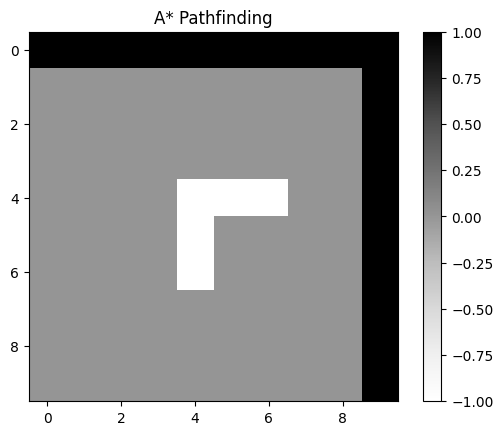
AO* 算法
AO*（And-Or）算法用于决策涉及多个子目标的问题。它通常用于涉及复杂问题解决的场景，其中一个动作可能导致多个结果。以下是一个带有可视化的简单示例
import networkx as nx
import matplotlib.pyplot as plt
def create_ao_graph():
G = nx.DiGraph()
G.add_edges_from([('Start', 'A'), ('Start', 'B'),
('A', 'C'), ('A', 'D'),
('B', 'D'), ('B', 'E'),
('C', 'Goal'), ('D', 'Goal'), ('E', 'Goal')])
return G
def plot_ao_graph(G):
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=2000, node_color='lightblue',
font_size=10, font_weight='bold', arrows=True)
plt.title("AO* Search Graph")
plt.show()
def ao_star_search(graph, start, goal):
# Simplified AO* search algorithm (pseudo-implementation)
path = []
nodes = nx.dfs_preorder_nodes(graph, source=start)
for node in nodes:
if node == goal:
path.append(node)
break
path.append(node)
return path
G = create_ao_graph()
plot_ao_graph(G)
path = ao_star_search(G, 'Start', 'Goal')
print("AO* Path:", path)
输出
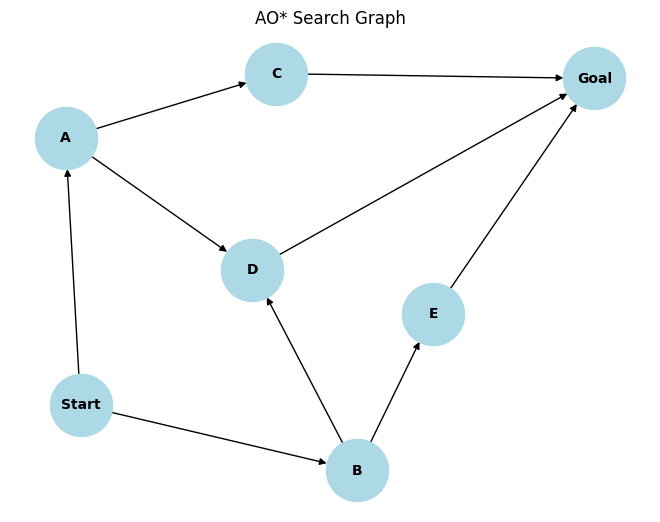
关于 A* 与 AO* 算法的常见问题
问：还有其他搜索算法吗？
答：当然！存在许多搜索算法，每种算法都有其独特的优势和劣势。深度优先搜索和广度优先搜索是两个流行的例子。
问：AO 能处理实时变化吗？
答：是的，AO* 被设计为能够有效地处理实时变化。
问：什么是启发式？
答：启发式类似于一种知情的估计。在 A* 算法中使用启发式来估计到目标的距离。它们通过将算法引导到正确的方向来提高其速度和效率。
结论
了解 A* 和 AO* 算法之间的区别可以帮助你更好地理解计算机如何解决一般问题，例如在游戏中确定最佳行动方案或在地图上找到最短路径。A* 专注于寻路，而 AO* 通过考虑不同的行动组合来解决决策问题。两者都是计算机科学领域中有效的工具，各自具有独特的优势。通过理解这些算法，你可以更好地理解计算机科学和人工智能中寻路和图遍历的复杂性。
1K+ 次浏览
