人工智能 - 常用搜索算法

搜索是人工智能中解决问题的通用技术。有一些单人游戏，例如拼图游戏、数独、填字游戏等。搜索算法可以帮助你在这些游戏中搜索特定位置。

单智能体寻路问题

像 3X3 八块拼图、4X4 十五块拼图和 5X5 二十四块拼图这样的游戏都是单智能体寻路挑战。它们由带有空白块的矩阵组成。玩家需要通过垂直或水平地将棋子滑入空白格来排列棋子，以达到某个目标。

单智能体寻路问题的其他例子包括旅行商问题、魔方和定理证明。

搜索术语

问题空间 - 搜索发生的场所。(一组状态和一组改变这些状态的操作符)
问题实例 - 初始状态 + 目标状态。
问题空间图 - 表示问题状态。状态由节点表示，操作符由边表示。
问题的深度 - 从初始状态到目标状态的最短路径或最短操作序列的长度。
空间复杂度 - 存储在内存中的最大节点数。
时间复杂度 - 创建的最大节点数。
可采纳性 - 算法始终找到最优解的属性。
分支因子 - 问题空间图中子节点的平均数量。
深度 - 从初始状态到目标状态的最短路径长度。

暴力搜索策略

它们是最简单的，因为它们不需要任何特定领域的知识。它们在可能状态数量较少的情况下效果很好。

要求：

状态描述
一组有效的操作符
初始状态
目标状态描述

广度优先搜索

它从根节点开始，首先探索相邻节点，然后移动到下一层邻居。它一次生成一棵树，直到找到解决方案。它可以使用 FIFO 队列数据结构实现。这种方法提供了到解决方案的最短路径。

如果分支因子（给定节点的子节点平均数量）= b，深度 = d，则 d 层的节点数 = b^d。

最坏情况下创建的节点总数为 b + b² + b³ + … + b^d。

缺点 - 由于每一层节点都保存下来以创建下一层节点，因此它会消耗大量内存空间。存储节点的空间需求呈指数级增长。

其复杂度取决于节点数。它可以检查重复节点。

深度优先搜索

它使用 LIFO 栈数据结构以递归方式实现。它创建与广度优先方法相同的节点集，只是顺序不同。

由于在每次迭代中从根节点到叶节点存储单路径上的节点，因此存储节点的空间需求是线性的。分支因子为 *b*，深度为 *m*，则存储空间为 *bm*。

缺点 - 此算法可能不会终止，并且会在一条路径上无限进行。解决这个问题的方法是选择一个截止深度。如果理想截止值为 *d*，而选择的截止值小于 *d*，则此算法可能会失败。如果选择的截止值大于 *d*，则执行时间会增加。

其复杂度取决于路径数。它不能检查重复节点。

双向搜索

它从初始状态向前搜索，从目标状态向后搜索，直到两者相遇以识别公共状态。

初始状态的路径与目标状态的反向路径连接。每次搜索仅进行到总路径的一半。

一致代价搜索

对到节点的路径成本按递增顺序进行排序。它总是扩展成本最低的节点。如果每个转换的成本相同，则它与广度优先搜索相同。

它按成本递增的顺序探索路径。

缺点 - 可能存在多个成本 ≤ C* 的长路径。一致代价搜索必须全部探索它们。

迭代加深深度优先搜索

它对第 1 层执行深度优先搜索，重新开始，对第 2 层执行完整的深度优先搜索，并以此类推，直到找到解决方案。

它只有在生成所有较低节点后才会创建节点。它只保存节点的堆栈。当它在深度 *d* 找到解决方案时，算法结束。在深度 *d* 创建的节点数为 b^d，在深度 *d-1* 为 b^d-1。

各种算法复杂度的比较

让我们根据各种标准查看算法的性能：

标准	广度优先	深度优先	双向	一致代价	迭代加深
时间	b^d	b^m	b^d/2	b^d	b^d
空间	b^d	b^m	b^d/2	b^d	b^d
最优性	是	否	是	是	是
完整性	是	否	是	是	是

启发式 (启发) 搜索策略

为了解决具有大量可能状态的大型问题，需要添加特定于问题的知识以提高搜索算法的效率。

启发式评估函数

它们计算两个状态之间最优路径的成本。滑动块游戏的启发式函数是通过计算每个块与其目标状态的移动次数并将所有块的这些移动次数相加来计算的。

纯启发式搜索

它按照启发式值的顺序扩展节点。它创建两个列表，一个用于已扩展节点的封闭列表和一个用于已创建但未扩展节点的开放列表。

在每次迭代中，扩展具有最小启发式值的节点，创建其所有子节点并将其放入封闭列表中。然后，将启发式函数应用于子节点，并根据其启发式值将其放入开放列表中。保存较短的路径，丢弃较长的路径。

A* 搜索

这是最著名的最佳优先搜索形式。它避免扩展已经很昂贵的路径，而是首先扩展最有希望的路径。

f(n) = g(n) + h(n)，其中

g(n) 到达该节点的成本（迄今为止）
h(n) 从该节点到达目标的估计成本
f(n) 通过 n 到达目标的路径的估计总成本。它使用优先级队列按 f(n) 递增实现。

贪婪最佳优先搜索

它扩展估计最接近目标的节点。它基于 f(n) = h(n) 扩展节点。它使用优先级队列实现。

缺点 - 它可能陷入循环。它不是最优的。

局部搜索算法

它们从一个潜在的解决方案开始，然后移动到一个相邻的解决方案。即使在它们结束之前任何时候中断，它们也可以返回一个有效的解决方案。

爬山搜索

这是一个迭代算法，它从问题的任意解开始，并尝试通过增量地更改解的单个元素来找到更好的解。如果更改产生了更好的解，则增量更改将作为新的解。重复此过程，直到没有进一步的改进。

函数爬山(问题)，返回局部最大值的状态。

inputs: problem, a problem
local variables: current, a node
                 neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
   do neighbor <- a highest_valued successor of current
      if Value[neighbor] ≤ Value[current] then
      return State[current]
      current <- neighbor				  
	
end

缺点 - 此算法既不完整也不最优。

局部束搜索

在此算法中，它在任何给定时间都保留 k 个状态。在开始时，这些状态是随机生成的。这些 k 个状态的后继者是借助目标函数计算的。如果这些后继者中的任何一个是目标函数的最大值，则算法停止。

否则，将（初始 k 个状态和状态的 k 个后继者 = 2k）个状态放入池中。然后对池进行数值排序。选择最高的 k 个状态作为新的初始状态。重复此过程，直到达到最大值。

函数束搜索( *问题，k*)，返回一个解状态。

start with k randomly generated states
loop
   generate all successors of all k states
   if any of the states = solution, then return the state
   else select the k best successors
end

模拟退火

退火是加热和冷却金属以改变其内部结构以修改其物理性质的过程。当金属冷却时，其新结构被固定，金属保持其新获得的性质。在模拟退火过程中，温度保持可变。

我们最初将温度设置得很高，然后随着算法的进行缓慢“冷却”。当温度很高时，允许算法以高频率接受较差的解。

开始

初始化 k = 0；L = 整数变量数；
从 i → j，搜索性能差异 Δ。
如果 Δ <= 0 则接受；否则，如果 exp(-Δ/T(k)) > random(0,1) 则接受；
对步骤 1 和 2 重复 L(k) 步。
k = k + 1；

重复步骤 1 到 4，直到满足条件。

结束

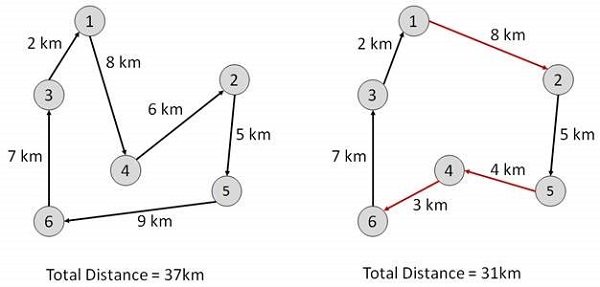
旅行商问题

在此算法中，目标是找到一个低成本的路线，从一个城市开始，沿途精确访问所有城市，并在同一起始城市结束。

Start
   Find out all (n -1)! Possible solutions, where n is the total number of cities.
   Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
   Finally, keep the one with the minimum cost.
end

打印页面