
人工智能 - 模糊逻辑系统
模糊逻辑系统 (FLS) 对不完整、模糊、失真或不准确(模糊)的输入做出可接受但明确的输出。
什么是模糊逻辑?
模糊逻辑 (FL) 是一种推理方法,类似于人类的推理。FL 的方法模仿人类决策的方式,包括“是”和“否”数字值之间的所有中间可能性。
计算机可以理解的常规逻辑块接受精确的输入并产生明确的输出,即 TRUE 或 FALSE,这相当于人类的“是”或“否”。
模糊逻辑的发明者 Lotfi Zadeh 观察到,与计算机不同,人类的决策包括“是”和“否”之间的一系列可能性,例如:
| 当然是的 |
| 可能是的 |
| 无法说 |
| 可能不是 |
| 当然不是 |
模糊逻辑基于输入的可能性级别来实现明确的输出。
实施
它可以应用于各种规模和功能的系统,从小型微控制器到大型的基于网络的工作站控制系统。
它可以以硬件、软件或两者的结合方式实现。
为什么使用模糊逻辑?
模糊逻辑对商业和实践用途很有用。
- 它可以控制机器和消费产品。
- 它可能不会给出准确的推理,但会给出可接受的推理。
- 模糊逻辑有助于处理工程中的不确定性。
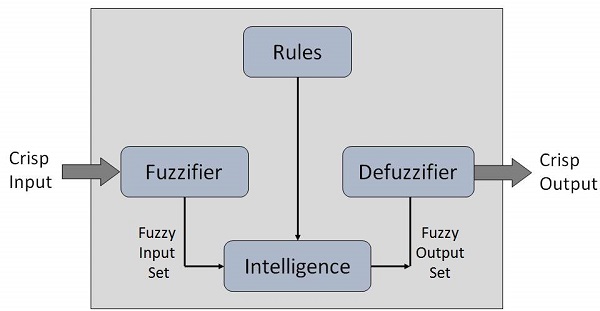
模糊逻辑系统架构
它有四个主要部分,如下所示:
模糊化模块 - 它将系统的输入(即清晰的数字)转换为模糊集。它将输入信号分成五个步骤,例如:
| LP | x 为大正 |
| MP | x 为中正 |
| S | x 为小 |
| MN | x 为中负 |
| LN | x 为大负 |
知识库 - 它存储专家提供的 IF-THEN 规则。
推理引擎 - 通过对输入和 IF-THEN 规则进行模糊推理,模拟人类推理过程。
反模糊化模块 - 它将推理引擎获得的模糊集转换为清晰的值。
隶属函数作用于变量的模糊集。
隶属函数
隶属函数允许您量化语言术语并以图形方式表示模糊集。模糊集 A在论域 X 上的隶属函数定义为 μA:X → [0,1]。
这里,X的每个元素都映射到 0 到 1 之间的值。它被称为隶属度或隶属程度。它量化了X中元素对模糊集A的隶属程度。
- x 轴表示论域。
- y 轴表示 [0, 1] 区间内的隶属度。
可以有多个隶属函数适用于将数值模糊化。使用简单的隶属函数,因为使用复杂的函数不会提高输出的精度。
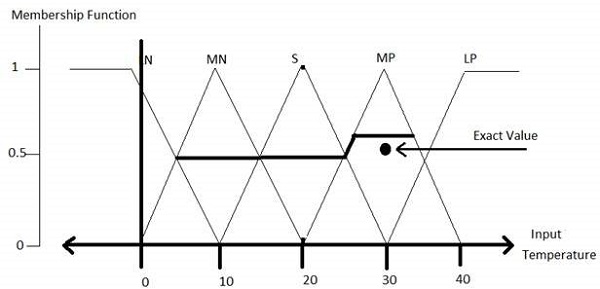
LP、MP、S、MN 和LN 的所有隶属函数如下所示:
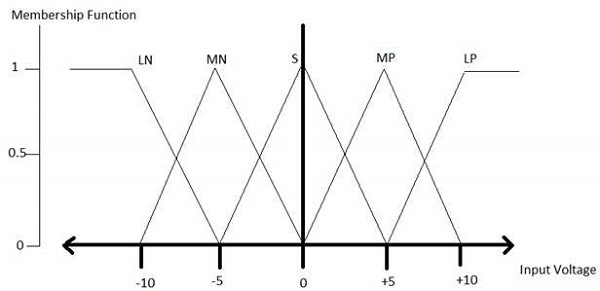
在各种其他隶属函数形状(如梯形、单点和高斯)中,三角形隶属函数形状最常见。
这里,输入到 5 级模糊器的范围为 -10 伏到 +10 伏。因此,相应的输出也会发生变化。
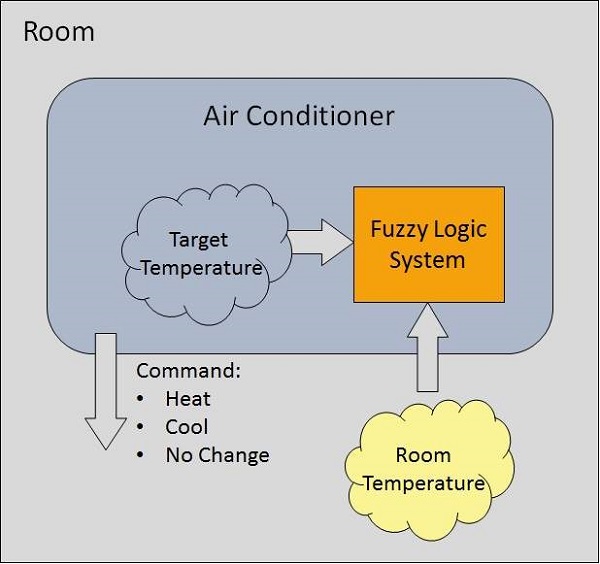
模糊逻辑系统示例
让我们考虑一个带有 5 级模糊逻辑系统的空调系统。该系统通过比较室温与目标温度值来调节空调的温度。
算法
- 定义语言变量和术语(开始)
- 为它们构建隶属函数。(开始)
- 构建规则的知识库(开始)
- 使用隶属函数将清晰数据转换为模糊数据集。(模糊化)
- 评估规则库中的规则。(推理引擎)
- 组合每个规则的结果。(推理引擎)
- 将输出数据转换为非模糊值。(反模糊化)
发展
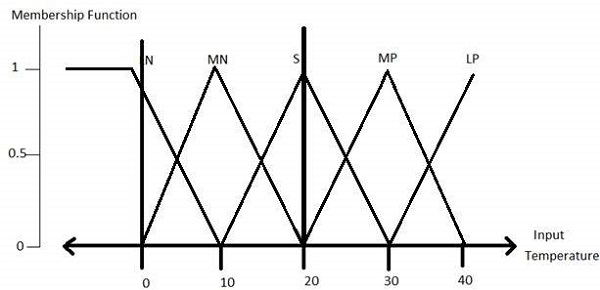
步骤 1 - 定义语言变量和术语
语言变量是以简单单词或句子的形式表示的输入和输出变量。对于室温,冷、暖、热等是语言术语。
温度 (t) = {非常冷、冷、暖、非常暖、热}
此集合的每个成员都是一个语言术语,它可以覆盖整体温度值的一部分。
步骤 2 - 为它们构建隶属函数
温度变量的隶属函数如下所示:
步骤 3 - 构建知识库规则
创建一个室温值与空调系统预期提供的目标温度值的矩阵。
| 室温/目标 | 非常冷 | 冷 | 暖 | 热 | 非常热 |
|---|---|---|---|---|---|
| 非常冷 | 无变化 | 加热 | 加热 | 加热 | 加热 |
| 冷 | 冷却 | 无变化 | 加热 | 加热 | 加热 |
| 暖 | 冷却 | 冷却 | 无变化 | 加热 | 加热 |
| 热 | 冷却 | 冷却 | 冷却 | 无变化 | 加热 |
| 非常热 | 冷却 | 冷却 | 冷却 | 冷却 | 无变化 |
将一组规则以 IF-THEN-ELSE 结构的形式构建到知识库中。
| 序号 | 条件 | 行动 |
|---|---|---|
| 1 | 如果温度 =(冷或非常冷)且目标 = 暖则 | 加热 |
| 2 | 如果温度 =(热或非常热)且目标 = 暖则 | 冷却 |
| 3 | 如果(温度 = 暖)且(目标 = 暖)则 | 无变化 |
步骤 4 - 获取模糊值
模糊集运算执行规则评估。用于 OR 和 AND 的运算分别是 Max 和 Min。组合所有评估结果以形成最终结果。此结果是一个模糊值。
步骤 5 - 执行反模糊化
然后根据输出变量的隶属函数执行反模糊化。
模糊逻辑的应用领域
模糊逻辑的关键应用领域如下所示:
汽车系统
- 自动变速箱
- 四轮转向
- 车辆环境控制
消费电子产品
- 高保真音响系统
- 复印机
- 静止和摄像机
- 电视
家用产品
- 微波炉
- 冰箱
- 烤面包机
- 吸尘器
- 洗衣机
环境控制
- 空调/干燥机/加热器
- 加湿器
FLSs 的优点
模糊推理中的数学概念非常简单。
由于模糊逻辑的灵活性,您可以通过添加或删除规则来修改 FLS。
模糊逻辑系统可以接收不精确、失真、嘈杂的输入信息。
FLSs 易于构建和理解。
模糊逻辑是解决生活各个领域(包括医学)中复杂问题的解决方案,因为它类似于人类的推理和决策。
FLSs 的缺点
- 模糊系统设计没有系统的方法。
- 它们只有在简单时才容易理解。
- 它们适用于不需要高精度的问 题。