等温过程与绝热过程的区别

---

引言

到目前为止，我们已知的科学划分并不局限于物理学、化学和生物学。随着我们对这些领域的深入研究，我们越来越需要将我们的知识分类到这三大类（物理学、化学和生物学）下的各个分支学科。例如，有机化学处理的是碳基化合物及其性质。

热力学就是物理学的一个分支。虽然热力学领域非常广泛，但我们将尝试在此总结其定义，然后讨论两种主要的热力学过程，即等温过程和绝热过程。

什么是热力学？

《大英百科全书》将热力学定义为“研究功、热、能量和温度之间关系的科学”。这是对热力学最简洁的描述。

“热力学”一词本身是由希腊词“therme”（热）和“dynamis”（力）复合而成。因此，从词源学角度来说，热力学是研究热力学的科学。

在热力学中，我们研究功、温度和热量如何与能量和熵相关联。我们还研究物质和辐射的物理性质如何影响热量和温度。我们对热力学的所有了解都可以快速总结成一套四条规则，通常称为热力学定律。

热力学定律

热力学定律可以用多种形式表达。然而，它们都是普遍有效的，并且尚未发现对其含义的例外。有趣的是，这些定律中的第一个被称为“第零定律”，而不是“第一定律”。让我们详细讨论一下。

第零定律

第零定律阐述了热平衡的等价性，并提供了一种经验性的方法来定义温度是什么。根据第零定律，如果你取两个与第三个系统处于热力学稳定状态的系统，那么它们也必须彼此处于热平衡状态。该定律与数学中的等价表达式相同。如果 A=C 且 B=C，则 A=B。

第一定律

第一定律表达了系统内能与热量和功之间的关系。其数学表达式如下：

$\mathrm{\Delta U = Q-W}$

这里，ΔU 是系统的内能变化，Q 是获得的热能，W 是系统对其周围环境所做的功。

第二定律

第二定律确定了 100% 效率的不可能。它指出：

“在循环过程中，不可能将所有热能都转化为功。”

第二定律可用于预测某个过程是否允许发生。有时，某个过程遵循能量守恒定律，但由于它使第二定律失效，因此仍然是被禁止的。

第三定律

第三定律预测了系统在接近绝对零度时的行为。简单来说，它指出当系统的温度接近绝对零度时，所有过程都会停止，其熵开始趋于一个常数值，该值可以为零，也可以不为零。

什么是等温过程？

系统温度保持不变的过程称为等温过程。“等温”一词源于希腊词根“isos”（相等）和“therme”（热）。

然而，有趣的是，虽然我们说温度必须保持恒定，但并没有对系统进出热量的限制。

等温过程的例子

相变

等温过程最常见的例子之一是相变。当固体变成液体或液体变成蒸汽时，系统会获得热量。然而，熔化和蒸发是等温发生的。

卡诺发动机

卡诺发动机有多个阶段，其中两个阶段涉及等温过程。冰箱基于卡诺循环，因此它们也涉及等温阶段。

等温过程中所做的功的表达式

所做功的热力学表达式如下所示。

$\mathrm{W=\int\:P \cdot dV}$

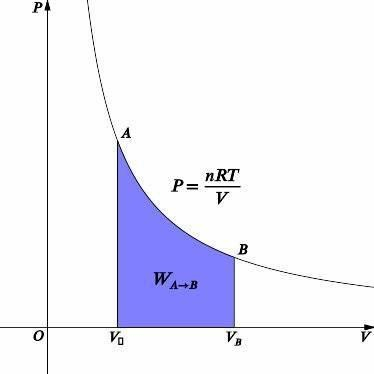
在等温过程中，我们知道温度是恒定的。等温过程的图表如上所示。使用理想气体方程，我们可以将压力和体积联系起来。

$\mathrm{PV = nRT}$

$\mathrm{P=\frac{nRT}{V}}$

现在，我们可以将此值代入所做功的表达式。

$\mathrm{W=\int\:\frac{nRT}{V} dV}$

由于摩尔数、温度和 R 是常数，我们可以将它们从积分中去掉。因此，

$\mathrm{W=nRT\:ln \:ln V |_{V_1}^{V_2}=nRT\:ln\:ln (\frac{V_2}{V_1})}$

因此，等温过程中所做的功由下式给出：

$\mathrm{W=nRT\:ln\:ln(\frac{V_2}{V_1})}$

什么是绝热过程？

“绝热”一词源于希腊语“adiabatos”，意思是不可逾越的。在这个过程中，不会发生热量或物质的转移。系统不会从其周围环境获得或损失热能，也不会交换物质。

极其快速发生的过程几乎没有热交换，因此在各种情况下都可以进行“绝热近似”，使它们易于求解。

绝热过程的例子

冰盒中的冰

为了使冰盒中的软饮料保持冰冷，我们把冰放在里面并盖上盖子。现在，热量不会进出系统，因此系统变成了绝热系统。

声音在空气中的传播

声音在气体中传播的速度非常快，因此没有时间发生热交换。因此，声音在气体中的传播是绝热过程。

绝热过程中所做的功

对于绝热过程，压力和体积之间的关系如下：

$\mathrm{PV^{\gamma}=K}$

其中 K 是一个常数。我们可以使用此关系来求解所做功的表达式：

$\mathrm{W=\int\:\:P \cdot dV=K \int \frac{1}{V-\gamma}dV=\frac{K}{1-\gamma}(V_2^{1-\gamma}-V_1^{1-\gamma})}$

可以使用理想气体方程得出 K 的表达式：

$\mathrm{P_1 V_1^{\gamma}=P_2 V_2^{\gamma}=K}$

$\mathrm{PV=nRT}$

因此，

$\mathrm{W=\frac{1}{1-\gamma}(P_2 V_2-P_1 V_1)}$

结论

热力学是研究热、功、温度及其与能量、熵和物质之间关系的科学。我们对热力学的了解可以总结成一套四条规则，称为热力学定律。

等温过程发生在温度不变的情况下，即使系统损失或获得热量。一个常见的例子是通过熔化将固体转变为液体。等温过程的功由以下方程给出：

$\mathrm{W=nRT\:ln\:ln(\frac{V_2}{V_1})}$

绝热过程定义为系统与其环境之间不传递热量或物质的过程。声音在空气中的传播速度太快，无法进行热交换，因此它是绝热的。在这种情况下，所做功的表达式是：

$\mathrm{W=\frac{1}{1-\gamma}(P_2 V_2-P_1 V_1)}$

常见问题

Q1. 等温过程和绝热过程的基本区别是什么？

A1. 等温过程在恒定温度下发生，但可以发生热交换。然而，绝热过程中不能发生热交换，即使温度发生变化。

Q2. 热交换如何在等温过程中发生？

A2. 当热量以极慢的速度流入或流出系统时，不会发生温度变化，因此该过程变为等温过程。

Q3. 冰箱是绝热系统吗？

A3. 不是。冰箱是等温系统。冰箱的内容物保持在恒定温度，热量被排出。

Q4. 所做功采用什么符号约定？

A4. 在物理学中，如果系统做了功，则热力学功为正；如果对系统做了功，则热力学功为负。

Q5. 绝热过程方程中的伽马 $\mathrm{(\gamma)}$ 项是什么？

A5. $\mathrm{\gamma}$ 代表绝热指数。要计算它，只需将恒压比热除以恒容比热。也就是说，$\mathrm{\gamma=\frac{C_p}{C_v}}$