光学显微镜和电子显微镜的区别

---

简介

借助我们的眼睛，我们可以看到我们周围美丽的自然世界。这是由于光线的作用。光线照射到任何物体上并被反射。这些反射光线进入我们的眼睛。眼睛有很多部分，比如角膜、房水和晶状体。从这里发出的光以电信号的形式通过视神经传到大脑。

但是，有些物体我们用肉眼无法看清。我们发现用眼睛很难看清遥远的行星和恒星。此外，像细胞、病毒或原子这样的小物体也无法用肉眼看到。因此，为了观察这些物体，我们需要借助一些仪器。这些被称为光学仪器。放大镜就是一个常见的例子。我们可以将它们分为两类——一类用于观察远处的物体，另一类用于观察微小的物体。

用于观察小物体或微小物体的装置称为显微镜。尽管有许多种类的显微镜，但在接下来的章节中，我们将学习光学显微镜和电子显微镜。

什么是光学显微镜？

它是一种使用可见光波的显微镜。这意味着光波从我们想要观察的物体上反射，然后进入我们的眼睛。最后，我们就能看到物体的放大图像。它也被称为光学显微镜。在这种显微镜中，我们使用可见光，波长在 400-700 纳米之间。

我们可以使用这种望远镜中的透镜进行放大。只有一个透镜的显微镜称为简单显微镜。复合显微镜有两个透镜。

光学显微镜的构造和工作原理

简单显微镜和复合显微镜是两种不同类型的显微镜。

• 简单显微镜 - 它由一个位于物体和眼睛之间的凸透镜组成。凸透镜放大物体，我们看到一个更大的图像。这是放大镜和目镜中使用的显微镜。

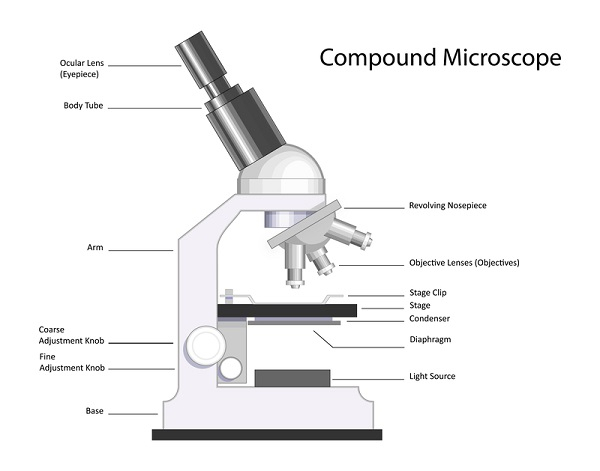
• 复合显微镜 - 在这种显微镜中，使用两个凸透镜。靠近物体的透镜称为物镜。它产生物体的实像。此图像形成在显微镜内部（图像 1）。靠近眼睛的透镜会产生此实像的放大图像（图像 2）。此透镜称为目镜。

光学显微镜的优缺点

优点	缺点
使用非常简单，便于携带	分辨率低
不受电磁辐射的影响	无法提供 3D 图像
允许用于活生物体	放大倍数不大
维护成本非常低	无法在黑暗中操作

什么是电子显微镜？

在电子显微镜中，我们使用电子束而不是可见光作为照明。如果我们使用电子束，则它们的波长大约比可见光的波长小 104 倍。因此，它比光学显微镜具有更高的分辨率。它不仅可以提供物体的图像，还可以告诉我们物体的结构。以下是一些主要的电子显微镜类型

• 透射电子显微镜

• 扫描电子显微镜

• 反射电子显微镜

• 扫描隧道显微镜

电子显微镜的构造和工作原理

电子显微镜的主要部件如下：

• 电子枪 - 这里使用钨丝，加热时会发射电子。

• 电磁透镜 - 使用聚光镜、物镜和投影镜。

• 载物台 - 由非常薄的碳片制成。

• 成像系统 - 相机位于荧光屏下方

电子枪用作电子源。第一个聚光镜将电子束聚焦到物体上，然后第二个聚光镜用于形成细电子束。反射后从物体发出的电子通过称为物镜的磁线圈。然后从投影镜获得最终图像。图像可以在荧光屏上看到。

电子显微镜的优缺点

优点	缺点
提供非常高的放大倍数	电子束会杀死活生物体
也可以创建 3D 图像	使用起来并不容易
高分辨率	电磁场的存在会影响图像。

结论

光学显微镜和电子显微镜都用于放大微小的物体。但是，它们之间存在一些差异。在光学显微镜中，我们使用可见光，而在电子显微镜中，使用电子束。电子显微镜的放大倍数和分辨率高于光学显微镜。

常见问题

Q1. 放大倍数是肉眼看到的物体高度与使用透镜后看到的物体高度之比。

答：$$\mathrm{m=\frac{h^{'}}{h}}$$

对于简单显微镜，放大倍数由下式给出：

$$\mathrm{m=1+\frac{D}{f}}$$

这里 D = 最近清晰视觉距离。

f= 透镜的焦距

Q2. 电子显微镜有哪些应用？

答：电子显微镜广泛应用于以下领域

• 在医学领域，用于活检样本和细胞研究等。

• 在工业中，它用于质量控制

• 晶体学家用它来研究晶体的内部结构。

• 在生物学中，它用于研究病毒、细菌等微生物。

Q3. 写出光学显微镜和电子显微镜的主要区别。

答：

光学显微镜	电子显微镜
使用光作为照明	使用电子束作为照明
可以观察活的或死的物体	主要用于死亡和干燥的样本
放大倍数是原始尺寸的 500 到 1500 倍	放大倍数是原始尺寸的 100000 到 300000 倍
物体的图像是有色的	物体的图像是黑白的
待研究的样品可在几分钟内制备好	待研究样品的制备时间可能需要几天。

Q4. 扫描电子显微镜和隧道显微镜有什么区别？

答：

扫描显微镜	隧道显微镜
它用于薄样品	它具有较大的深度
通过样品的透射电子形成物体的投影图像。	由样品产生的二次电子形成图像。
类似于传统的复合显微镜	类似于立体光学显微镜
易于使用	需要培训
样品制备简单	样品制备费力

Q5. 我们能否改变复合显微镜的放大倍数？如何？

答：复合显微镜的放大倍数由下式给出：

$$\mathrm{m=-\frac{L}{f_{0}}\frac{D}{f_{e}}}$$

其中 L = 显微镜筒长或目镜与第二透镜之间的距离

D = 最近清晰视觉距离

$\mathrm{f_{0}}$ = 物镜的焦距

$\mathrm{f_{e}}$ = 目镜的焦距

如果我们增加显微镜筒长，我们可以增加复合显微镜的放大倍数。因为放大倍数与显微镜筒长成正比。我们还可以看到，使用短焦距的透镜也会增加显微镜的放大倍数。