标量和矢量的区别

---

介绍

可以使用代数原理来解释矢量和标量。标量表示一维值，而矢量表示二维或多维值。物体的运动也可以用矢量和标量来表示。

什么是标量？

标量是物理学中一个重要的数学表达式。这个物理学领域与测量有关。米和度是两个最重要的测量单位，用于表示标量单位的值（Sirunyan 等人，2018）。数值用于表示标量的值。大小和数量级是标量的相关术语。

标量的例子

• 电荷密度

• 质量

• 温度

• 万有引力

• 电荷

• 体积

• 时间

什么是矢量？

在矢量中，方向和数量级作为两个独立的属性。数量级用于表示矢量的大小。方向用于表示任何物体运动方向。矢量与“三角形法则”相关（Shadmi 和 Weiss，2019）。由于方向是矢量的属性，因此矢量可以是二维甚至三维的。

图 1：矢量和标量的区别

根据上图，汽车的速度是标量。速度表示为汽车的矢量。计算出的 45 公里/小时的速度是速度的值，它是一个矢量。

• 力

• 电场

• 加速度

• 速度

• 极化

• 位移

• 线性动量

矢量表示法

直角坐标系表示法 - 矢量位于一个重要且显著的直角坐标系中。几何表示如下所示

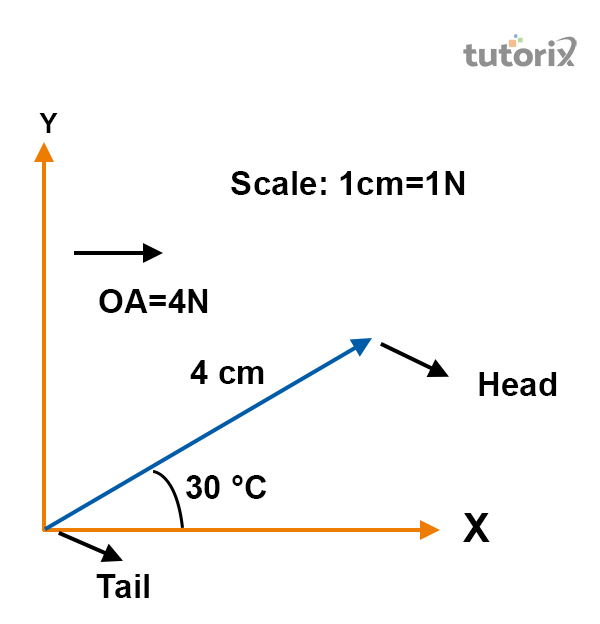
图 2：矢量的表示

如上图所示，矢量位于 X 轴和 Y 轴上。矢量与 X 轴之间形成的角度为 300 度。矢量计算为 4 厘米。

矢量加法

在某些情况下，可以按照一些基本规则以几何方式添加矢量。加法过程取决于一些因素。矢量的每个行为特征都是根据其自身特性确定的（Alonso-Álvarez、Hugle 和 Jaeckel，2020）。作用在特定物体上的不同矢量的结果被视为矢量加法过程。交换律是矢量加法的重要组成部分。交换律的方程如下：

$$\mathrm{\overrightarrow{A} + \overrightarrow{B} = \overrightarrow{B} + \overrightarrow{A}}$$

矢量减法

两个矢量的减法可以通过将两个矢量的起点放在一起完成。然后绘制一个结果矢量来进行矢量减法。

标量和矢量的区别

不同的参数	矢量	标量
含义	矢量既有方向又有数量级。	标量没有方向，只有数量级。
变化	当数量级、方向或两者都发生变化时，矢量会发生变化。	只有数量级的变化才会导致标量的变化。
数量	两个或多个矢量的数学运算结果可以是标量或矢量。	两个或多个标量的数学运算结果只会产生标量。标量和矢量的运算结果是矢量。
运算	两个或多个矢量的数学运算结果可以是标量或矢量。	两个或多个标量的数学运算结果只会产生标量。标量和矢量的运算结果是矢量。
分解	可以使用正弦或余弦根据相邻角轻松地将矢量分解到任何不同的方向（Baumann 等人，2020）。	由于方向相同，标量不能被分解。
表达式	粗体字母（例如 V）用于表示速度的值。添加箭头也是表达矢量值的重要方法。	标量值用简单的字母表示，例如 V 表示速度。
除法	矢量不能被任何其他矢量除。	标量可以很容易地被另一个标量除。
测量	矢量值的测量方式比较复杂。	标量值的测量比矢量值简单。

标量和矢量的相似之处

• 矢量和标量都具有有限的数量级。

• 矢量和标量都可以用合适的仪器测量。

• 它们都有特定的单位和维度（Zou 和 Myung，2019）。

• 标量和矢量都用某些物理量来表示。

结论

在描述任何物理量时，都需要数量级和方向。此时矢量是相关的。标量的计算使用代数的一些标准规则，如乘法、加法和减法。矢量遵循代数原理。

常见问题

Q1. 电流不是矢量的原因是什么？

电流的方向与电子流的方向相反。电流既有方向又有数量级。因此，电流是标量。

Q2. 单位矢量的数量级是多少？

单位矢量没有维度。单位矢量的数量级为 1。单位也被认为是“单位矢量的数量级”。

Q3. 是否可以将两个矢量相加？

不能将两个不同的矢量相加。组合时需要具有相同性质、类型和特征的矢量。例如，一个力矢量不能与一个速度矢量组合，而两个力矢量可以组合。

Q4. 定义矢量时必须注意什么？

矢量的定义需要指定方向。速度、重量、位移和力都是矢量的例子。