标量积与向量积

---

介绍

标量积可以用数值或大小来衡量，而向量积则用大小和方向来描述。根据物理学规则，一个标量和两个向量可以相乘，形成两种类型的积。标量积和向量积都用于定义能量和所做的功，尤其是在能量关系中。

标量积和向量积的定义

标量积可以定义为一种代数运算，它涉及两个长度相等的数字序列，结果每次只返回一个结果。这个积可以通过将一个向量向另一个向量的某个方向的分量与另一个向量的大小相乘来求得 (Pellicer & Sola-Morales, 2019)。距离、质量、体积、能量和长度等都是标量积的例子。

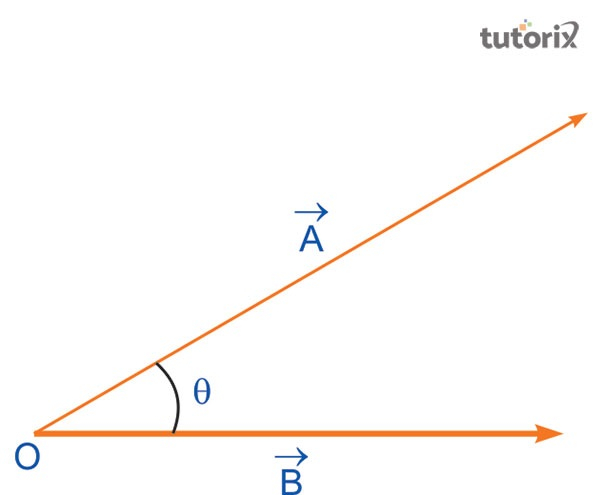
图1：标量积

用数学方程式表示标量积，公式为“$\mathrm{\vec{A}.\vec{B} \:= \:|\vec{A}| |\vec{B}|\: cos \:\phi}$”。在这个公式中，$\mathrm{|\vec{A}|}$ 是向量 A 的大小，$\mathrm{|\vec{B}|}$ 是向量 B 的大小，$\mathrm{\phi}$ 是向量 A 和向量 B 之间的角度。在解释物理学中的标量时，标量积也定义为两个向量的点积。向量$\mathrm{(^\vec{})}$可以定义为具有大小和方向的对象。向量积可以用表示大小长度和方向的箭头来表示。向量通常从尾部指向头部，具有其大小。通常，向量积由于与三维空间的结合，也称为面积积或叉积。

图2：向量积

向量通常表示为“$\mathrm{\vec{a} \:x \:\vec{b}}$”，其中积的结果垂直于原始向量。为了演示向量积，物理学中使用公式“$\mathrm{\vec{A} \:x \:\vec{B}\: =\: |\vec{A}||\vec{B}|sinθn}$”。在这个公式中，$\mathrm{|\vec{A}|}$ 是向量 A 的大小，$\mathrm{|\vec{B}|}$ 是向量 B 的大小，θ是向量 A 和向量 B 之间的角度，最后 n 是垂直于向量 A 和向量 B 的单位向量 (Hyperphysics, 2022)。

标量积和向量积的性质

标量积有一些独特的性质，使其在实时应用中非常有用。首先，就标量积而言，方程式中两个向量之间的角度方向没有任何意义。它只能从一个向量测量到另一个向量，因为$\mathrm{cos\:\theta \: = \: cos \:(-\theta) \: = \: cos\:\theta (2\pi - \theta)}$。标量积中的角度大于90°，小于或等于180°时，积为负值。因此，标量积的数学方程为$\mathrm{90^{\circ}\:\lt\: \theta \:\lt\: = \:180^{\circ}}$。

另一方面，向量积有两个显著的性质，使其与标量积区别开来。首先，大多数向量积都基于右手螺旋定则来获得实时所需的正确方向 (Sun *et al.*, 2021)。最重要的是，向量积是非交换的，这可以从其数学方程$\mathrm{\vec{b}\:x\:\vec{a}\:=\:-a\:x\:\vec{b}}$中得出。

图3：三维向量

向量积的另一个重要性质是它对加法的分配性。这一特性与标量积的特性相同，这可以在点积中看到。向量也包含基于点积的网关的三维结构 (Thefactfactor, 2022)。最后，可以说，当向量的方向在实时改变时，向量积可以改变，但仍然是等价的。

标量积和向量积的区别

尽管标量积和向量积之间存在着内在的联系，但它们却截然不同。第一个区别出现在积的表示中，标量积用点表示，向量积用叉表示。此外，标量积的关系定义为“$\mathrm{\vec{A}.\vec{B}\:=\:AB\:Cos\:\theta}$”，向量积定义为“$\mathrm{\vec{A}\:\times\:\vec{B}\:=\:AB\:Sin\:\theta}$”。

最重要的是，标量积遵循交换律，而向量积则完全不服从交换律。最后，标量积彼此垂直，值为 A.B = 0 (Geeksforgeeks, 2022)。另一方面，向量积彼此平行，值为“$\mathrm{\vec{A}x \:\vec{B} = 0}$”。

结论

标量积可以定义为一次对两个向量的乘法运算。另一方面，向量积用于定位空间中某点相对于空间中另一点的特定位置。尽管它们有相似之处和内在的联系，但这些积在实时应用中用不同的数学方程式来表示。

常见问题

Q1. 标量积和向量积之间有什么关系？

A1. 标量积和向量积常用于工程和物理学，因为它们都可以在数学乘法后使用。在某种程度上，标量积是基于实时的向量，所以它们之间建立的关系是基于功和能量的。

Q2. 向量在实时应用中的用途是什么？

A2. 向量对于通过附加规则表示方向和大小至关重要。在定义速度方面，它在概述实时速度的大小方面起着关键作用。

Q3. 标量积和向量积是如何表示的？

A3. 根据其独特的特性，标量积称为点积，向量积称为叉积。因此，标量积用点(.)表示，向量积用叉(x)表示。