标量积

---

介绍

标量积对于理解矢量量在实时中的运动至关重要。这些积可以同时相减或相加，并使用适当的代数公式来理解不同物体的标量量。这些类型的积通常根据其特征表示为内积或点积，以通过点来概述标量乘法。

标量积的定义

标量积定义为由两个向量的幅值与不同向量之间余弦角的乘积。标量积主要涉及两个数字序列的对应项乘积的和。这些积在力学、工程和几何方面有各种应用（Cavaglia等，2019）。

简单来说，标量积可以定义为具有两个不同向量和它们之间一个角的幅值的乘积。

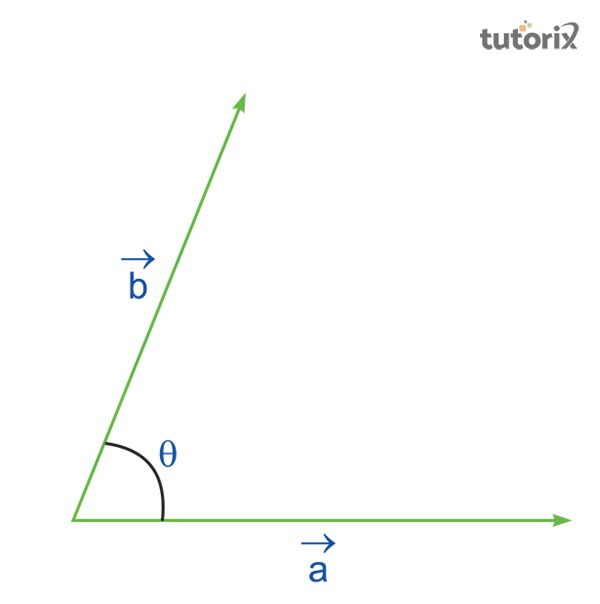
图 1：标量积示例 1

例如，如果$\mathrm{\vec{a}}$和$\mathrm{\vec{b}}$是两个具有特定幅值|a|和|b|以及角度θ的非零向量，则太阳积的代数运算将为“$\mathrm{\vec{a}.\vec{b} \:= \:|a| |b| \:cos\: θ}$”。此处，表达式根据标量积规则表示0 ≤ θ ≤。此处，a 或 b 等于 0，尤其是在方程式中未定义 θ 时。在这种情况下，此标量积中的 a 和 b 均显示为等于 0（Sciencedirect，2022）。

因此，如果向量 a 和向量 b 的值等于 0，则向量 a.b 的值也为 0。

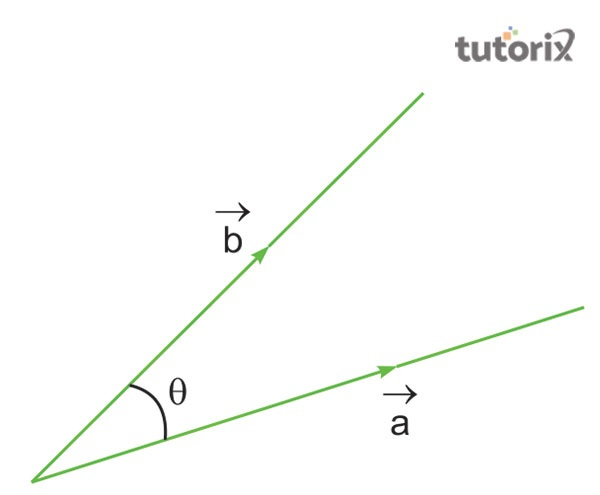
图 2：标量积示例 2

在第二个示例中，可以看出，如果绘制两个向量“$\mathrm{\vec{a}}$和“$\mathrm{\vec{b}}$到标量积的θ，则标量积可以显示为$\mathrm{\vec{a}.\vec{b} \:= \:|a| |b| \:cos\: θ}$。此处，|a|是向量 a 的幅值，|b|表示向量 b 的模数，θ表示向量 a 和向量 b 之间的角度（Mathcentre，2022）。

由于标量积的符号表示为点，因此在实时使用时，它进一步表示为点积。面积、体积、功、能量、压力、质量、密度、时间和距离等分量是标量积的主要示例。

标量积的矩阵表示

标量积在矩阵上的表示可以使用两种不同的模式完成，即列矩阵和行矩阵。标量积的单位向量通常可以是空间的，在列矩阵中具有不同的向量。此处，矩阵包含 x、y 和 z 等分量，以转置行矩阵中的向量（Pei & Terras，2021）。例如，如果 A 和 B 是标量积矩阵中存在的两个不同向量，则这两个矩阵将协作一次仅提供一个数字作为两个向量在标量积内加减的结果。

$$\mathrm{(A_X | A_Y | A_Z)\begin{pmatrix}B_X \B_Y \B_Z \\end{pmatrix} \:=\: A_X B_X+A_Y B_Y+A_Z B_Z \:=\: \vec{A}. \: \vec{B}}$$

通常从标量矩阵中提取的单个数字通常包含乘积的总和，尤其是在对应于一次多个向量的空间分量时。因此，标量积的矩阵表示以一个著名的过程表示，该过程用于在某个元素内的矩阵乘法中。此处，乘积的和以列和行格式显示，并在实时标量积中显示某个给定数字。

标量积的特征

标量积具有一些独特的特征，使它们在实时中与向量积不同。标量积的主要特征是交换性和分配性。

此处，标量属性的计算以不同的顺序进行，从向量 b 开始到向量 a，与一般的标量积完全相反。除此之外，这种类型的乘积通常遵循分配律，可以在三个连续的向量 a、b 和 c 中隐含。

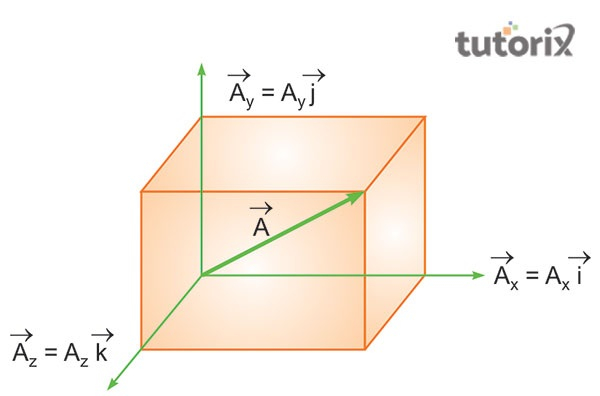
图 3：标量积的特征

标量积可以根据其大小以及与实时向量加减相关的代数解来定义。标量积的另一个特征是向量在一次手动垂直站立，尤其是在两个向量的值仅为 0 时（Thefactfactor，2022）。最后，根据标量积的交换律，向量的幅值的平方等于向量的自积。

结论

标量积是交换积，并结合了等长数字序列。这些积通常在一次获取两个向量后仅返回一个数字。最重要的是，标量积可以根据数学表示方面的代数方程彼此相减和相加。此外，标量积是通信积，直接参与实时向量分量的改变。

常见问题

Q1. 标量积的代数公式是什么？

答：标量积的代数公式为 |a| |b| cos θ。该公式依赖于两个向量，向量 a 和向量 b，并遵循 |a| 和 |b| 的幅值。

Q2. 标量积遵循哪些定律？

答：标量积通常遵循两个独特的规则，即交换律和分配律。这些积的分布遵循与加法相关的途径，而交换律遵循交换途径。

Q3. 实时标量积的一些示例是什么？

答：标量积具有从决定路线和在特定地点搜索路线开始的实时用途。除此之外，这些产品在现实生活中计算勾股定理的领域也有主要用途。