递减余额法计算折旧

电力设备折旧

电力站设备及其他财产每年价值的减少称为折旧。因此，必须每年留出适当的金额，称为*折旧费用*，以便在发电厂寿命结束时，所收集的金额等于发电厂更换成本。

递减余额法折旧

在递减余额法中计算折旧时，每年按设备递减价值的固定比率计提折旧费，即折旧费首先用于设备的初始成本，然后用于其递减价值。

例如，假设设备的初始成本为 100000 卢比，其使用寿命后的残值是 0。如果每年的折旧率为 10%。那么，第一年的折旧费将是

$$\mathrm{第一年折旧费用 = 100000 \times 10\% \, =\, 10000 卢比}$$

因此，设备的价值减少了 10000 卢比，变为 90000 卢比。

第二年，折旧费将按递减值（即 90000 卢比）计算，结果是：

$$\mathrm{=90000\times 10\%\, =\, 9000 卢比}$$

现在，设备的价值变为 90000 - 9000 = 81000 卢比

同样，第三年的折旧费将是：

$$\mathrm{= 81000 \times 10\% \, =\, 8100 卢比}$$

数学解释

设

• 𝑃 = 设备的初始成本
• 𝑆 = 设备使用寿命后的残值
• 𝑛 = 设备的使用寿命（年）
• 𝑥 = 年折旧率

那么，设备一年后的价值是：

$$\mathrm{一年后价值 = 𝑃 - 𝑃x = 𝑃(1 - x)}$$

设备两年后的价值是：

$$\mathrm{两年后价值 = 递减价值 - 年折旧}$$

$$\mathrm{\Rightarrow 两年后价值 = (𝑃 - 𝑃x) - [(𝑃 - 𝑃x)x]}$$

$$\mathrm{\Rightarrow 两年后价值 = (𝑃 - 𝑃x)(1 - x) = 𝑃(1 - x)(1 - x)}$$

$$\mathrm{\therefore 两年后价值 = 𝑃(1 - x)^2}$$

因此，𝑛 年后设备的价值是：

$$\mathrm{𝑛 年后价值 = 𝑃(1 - x)^n}$$

此外，设备使用寿命（即 n 年）后的价值等于残值 (S)。

$$\mathrm{\therefore S = 𝑃(1 - x)^n}$$

$$\mathrm{\Rightarrow (1 - x)^n = \frac{S}{P}}$$

$$\mathrm{\Rightarrow (1 - x) = \left( \frac{S}{P} \right)^{\frac{1}{n}}}$$

$$\mathrm{\therefore x = 1 - \left( \frac{S}{P} \right)^{\frac{1}{n}}}$$

上述表达式给出年折旧率的值。

因此，第一年的折旧费由下式给出：

$$\mathrm{第一年折旧费用 = 𝑃x = 𝑃\left[ 1 - \left( \frac{S}{P} \right)^{\frac{1}{n}} \right]}$$

同样，可以计算任何年限的年度折旧费。

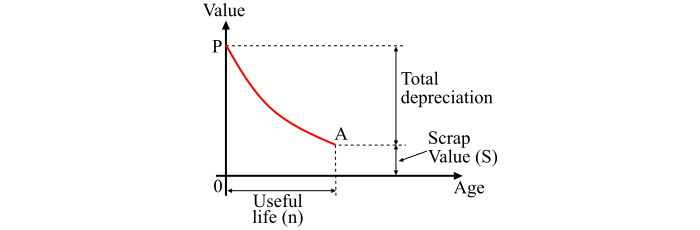
图中显示了用于计算折旧的递减余额法的图形表示。从图中可以清楚地看出，设备的初始值通过折旧减少到设备使用寿命内的残值。因此，折旧曲线遵循 PA 路径。此外，还可以观察到，早期年份的折旧费用较高，但在后期年份则降低到较低的值。

递减余额法存在以下缺点：

• 后期年份的折旧费用较低，而维护费用却很高。

• 折旧费与累积期间可能产生的利息率无关。此类利息应视为收入。

数值示例

一台变压器成本为 150000 卢比，25 年后的残值为 15000 卢比。使用递减余额法确定变压器 20 年后的折旧值。

解答

已知：

• 变压器的初始成本，𝑃 = 150000 卢比
• 变压器的残值，𝑆 = 15000 卢比
• 使用寿命，𝑛 = 25 年

则，年折旧率：

$$\mathrm{x = 1 - \left( \frac{S}{P} \right)^{\frac{1}{n}} = 1 - \left( \frac{15000}{150000} \right)^{\frac{1}{25}}}$$

$$\mathrm{\therefore x = 1 - 0.912 = 0.088}$$

因此：

$$\mathrm{20 年后变压器的价值 = 𝑃(1 - x)^{20} }$$

$$\mathrm{= 150000 \times (1 - 0.088)^{20} = 23767.74 卢比}$$

Saini Manish Kumar

更新于：2022 年 2 月 9 日

4000+ 浏览量

启动您的职业生涯

通过完成课程获得认证

开始