位移电流

---

介绍

最初，电和磁被视为独立的学科。后来，由于奥斯特、法拉第、麦克斯韦等人的贡献，它们发展成为一个统一的学科。载流导线在其周围产生磁场。法拉第通过他的实验表明，即使电路中没有电池，也可以产生电流。磁场的变化可以在电路中产生电流。这个结果被称为电磁感应。麦克斯韦试图以统一和紧凑的方式写出电磁学的所有主要方程。这些方程被称为麦克斯韦方程组。

这组方程包括：静电的高斯定理、磁的高斯定理、安培环路定理和法拉第电磁感应定律。麦克斯韦发现安培定律存在一些不一致之处。他修改了这个方程，并引入了一个新的概念，称为位移电流。因此，这个方程有时也被称为麦克斯韦-安培方程。

什么是位移电流？

詹姆斯·克拉克·麦克斯韦引入了这个概念。如果在一个区域内有电荷流动且存在电流，那么由于电流的存在，就会产生磁场。根据麦克斯韦的理论，在空间中，磁场是由位移电流产生的。与传统电流不同，它不是由电荷组成的。由于电容器极板之间存在自由空间，我们可以通过以电容器为例来推导出位移电流的表达式。

位移电流方程

为了得到位移电流方程，我们以电容器为例。我们尝试使用安培定律来求解磁场 -

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}i_{enc}}$$

其中 B = 磁场，i = 通过表面的净电流。

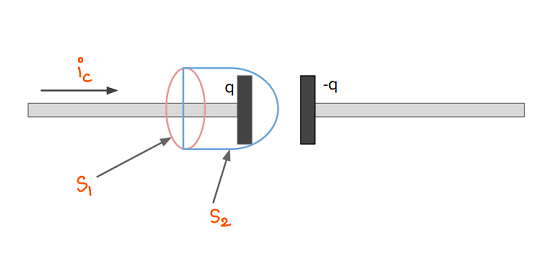
首先，我们尝试通过取表面 $\mathrm{S_{1}}$ 来计算磁场。通过该表面的电流为 $\mathrm{i_{c}}$。因此，根据安培定律，将存在一些磁场。如果我们取表面 $\mathrm{S_{2}}$，那么将没有电流通过该表面。这意味着 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 同时为零和非零。这是一个矛盾的结果。

麦克斯韦通过引入位移电流解决了这个问题。

$$\mathrm{i_{d}=\epsilon _{0}\frac{d \phi _{E}}{dt}}$$

这里 $\mathrm{i_{d}}$= 位移电流

$\mathrm{\phi _{E}}$ = 电通量

我们可以将此项包含在安培定律中。

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}(i_{c}+i_{d})=\mu _{0}i_{c}+\mu _{0}\epsilon _{0}\frac{d\phi _{E}}{dt}}$$

它被称为麦克斯韦-安培方程。

如果我们使用此关系，我们可以解决电容器问题中产生的歧义。

对于表面 $\mathrm{S_{1}:i=i_{c}}$ 且 $\mathrm{i_{d}=0}$，因为电通量没有变化。

对于表面 $\mathrm{S_{2}:i=i_{d}}$ 且 $\mathrm{i_{c}=0}$，因为没有电荷。

因此，现在两个表面的磁场将不为零。

位移电流的特性

位移电流是由变化的电通量产生的。它可以写成 -

$$\mathrm{i_{d}=\epsilon _{0}\frac{d\phi _{E}}{dt}}$$

它具有以下特性 -

• 它是矢量量。

• 它以安培为单位测量，其量纲与传统电流相似。

• 它不是由电子的流动产生的，而是由电场的变化产生的。

• 它不遵循欧姆定律。

• 对于闭合路径，它为零。

• 它不是实际电流。

位移电流的应用

我们可以使用位移电流计算圆形电容器内部的磁场。

假设电容器极板的半径为 R，然后我们想象在这些极板之间有一根半径为 R 的圆形导线。我们将流过导线的电流等于位移电流 $\mathrm{i_{d}}$。我们可以在此处使用安培环路定律。由于极板之间只有位移电流 -

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=B\oint dl=B2\pi r}$$

r= 磁场点到中心的距离。

电流均匀分布，环路包围的电流 $\mathrm{i_{enc}}$ 与环路包围的面积成正比。因此

$$\mathrm{i_{enc}=i_{d}\frac{\pi r^{2}}{\pi R^{2}}}$$

这意味着

$$\mathrm{B2\pi r=\mu _{0}i_{enc}}$$

$$\mathrm{B2\pi r=\mu _{0}i_{d}\frac{\pi r^{2}}{\pi R^{2}}}$$

$$\mathrm{B=(\frac{\mu _{0}i_{d}}{2\pi R^{2}})r}$$

它是电容器内部的磁场。它与电容器极板半径的平方成反比，与磁场点到中心的距离成正比。

我们还可以计算圆形电容器外部的磁场，它将是 -

$$\mathrm{B=\frac{\mu _{0}i_{d}}{2\pi r}}$$

结论

麦克斯韦发现安培定律存在一些不一致之处。他通过引入一种称为位移电流的电流修改了该方程。位移电流不是由电荷的流动产生的，而是由变化的电通量产生的。它的单位和量纲与传统电流相同。

常见问题解答

Q1. 写下麦克斯韦电磁方程组。

答：麦克斯韦电磁方程组如下 -

• $\mathrm{\oint \overrightarrow{E}.\overrightarrow{dA}=\frac{q_{enc}}{\epsilon _{0}}}$，它将净电荷与电通量联系起来。

• $\mathrm{\oint \overrightarrow{E}.\overrightarrow{dA}=0}$，它将净磁荷与磁通量联系起来。

• $\mathrm{\oint \overrightarrow{E}.\overrightarrow{dA}=-\frac{d\phi _{B}}{dt}}$，它将磁通量的变化与感应电场联系起来。

• $\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}i_{c}+\mu _{0}\epsilon _{0}\frac{d\phi _{E}}{dt}}$，它将感应磁场与电流联系起来。

Q2. 半径为 2cm 的圆形电容器的位移电流为 4A，求电容器内部距离 R/4 处的磁场。

答：已知 R = 2cm = $\mathrm{2\times 10^{-2}m}$

$$\mathrm{I = 4A}$$

$$\mathrm{r=\frac{R}{4}}$$

我们可以使用我们在上一节中推导出的公式 -

$$\mathrm{B=(\frac{\mu _{0}i_{d}}{2\pi R^{2}})r}$$

$$\mathrm{B=\frac{4\pi \times 10^{-7}\times 4}{2\pi \times R^{2}}\frac{R}{4}=\frac{2\times 10^{-7}\times 4}{R\times 4}}$$

$$\mathrm{B=\frac{2\times 10^{-7}}{2 \times 10^{-2}}=10^{-5}}$$

$$\mathrm{B=10^{-5}T}$$

Q3. 说明安培环路定理。

答：安培定律可以这样陈述：“穿过任何包含稳恒电流的闭合回路的磁场力的线积分与穿过该回路的电流成正比。”

假设存在一个闭合路径 C，并且穿过它的净电流为 $\mathrm{i_{enc}}$。然后我们可以写

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}i_{enc}}$$

Q4. 一个平行板电容器的电势为 100 V。如果极板之间的距离为 $\mathrm{}$𝟐。计算 $\mathrm{}$ 的位移电流。

答：平行板电容器的电势 V = 100V

极板之间的距离 d = 2mm = $\mathrm{2\times 10^{-3}mm}$

$$\mathrm{极板面积 A\:=\:20\times 10^{-4}m^{2}}$$

$$\mathrm{时间 t=2μs=2\times 10^{-6}s}$$

$$\mathrm{位移电流 i_{d}=\epsilon _{0}\frac{d\phi }{dt}=\epsilon _{0}\frac{EA}{t}}$$

我们知道 $\mathrm{E=\frac{v}{d} }$

$$\mathrm{因此，i_{d}=\epsilon _{0}\frac{vA }{dt}=8.85\times 10^{-12}\frac{10^{2}\times 20\times 10^{-4}}{2\times 10^{-3}\times 10^{-6}\times 2 }}$$

$$\mathrm{i_{d}=\frac{8.85\times 5\times 10^{-16}}{10^{-9}}=8.85\times 5\times 10^{-7}}$$

$$\mathrm{i_{d}=44.25\times 10^{-7}A}$$

$$\mathrm{i_{d}=4.4μA}$$

Q5. 位移电流的存在是否需要电场的变化？

答：如果电通量发生变化，则可能存在位移电流。在某些情况下，电场可能没有变化，但总通量却在变化。