位置、路径长度和位移

---

引言

如果任何物体的相对位置随时间变化，则称其处于运动状态。任何物体的运动都以三种方式发生，例如一维运动、二维运动和三维运动。火车在直轨上的运动和陀螺的圆周运动都是运动的例子。粒子的运动最好用力学定律来描述。为了理解物体的运动，提出了三个定律。当有运动时，就会有位移。

什么是运动？

如果粒子从一个地方移动到另一个地方，那么它就在运动中。线性运动是粒子相对于时间沿直线路径（称为线性运动）从一个地方移动到另一个地方的运动。因此，线性运动也可以定义为位移随时间的变化。如果粒子的运动沿直线，则称其为线性运动。如果粒子的运动是沿圆周路径，则称其为圆周运动或轨道运动。它也被称为角运动。推箱子和子弹从枪中射出都是线性运动的例子。地球自转、铁饼投掷和系在绳子上的石头的运动都是旋转运动或角运动的例子。

解释位置和路径长度

位置

位置的变化表示运动。直角坐标系用于定义物体位置的坐标。有三个轴通过一个称为原点 (O) 的点。它们是 x、y 和 z 轴，彼此垂直。物体的 位置取决于物体的运动。例如，如果物体进行一维运动，则物体的位置只需要一个坐标。

类似地，对于三维运动，需要三个坐标。沿 x 轴的物体位置是通过取零点作为参考点来计算的。位于零点右侧的物体位置取为正，左侧取为负。

路径长度

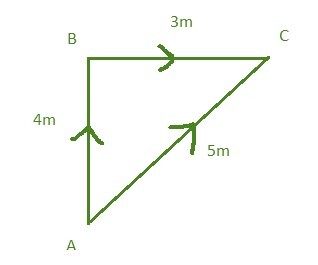
物体初始位置和最终位置之间的距离表示路径长度。在下图中，让我们考虑自行车从 A 到 B 的运动。自行车从 A 到 B 的距离为 4 米。让我们考虑一下，自行车从 A 移动到 B，然后从 B 移动到 C，然后从 C 移动到 A。自行车行驶的总距离或路径长度为 4 + 3 + 5 = 12 米。如果物体沿圆周路径移动，则物体行驶的总距离由 2πr 给出。

位移及示例

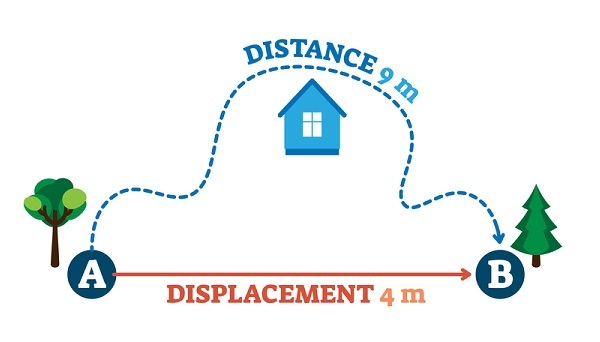
如果粒子从一个位置移动到另一个位置，则称该粒子处于运动状态。在一定时间内按照运动方向行进的距离称为位移。因此，位移是矢量量。箭头标记用于表示位移的方向。因为它是一个矢量量，所以它的方向是用箭头标记表示的。让我们考虑一下球从一个地方移动到另一个地方的运动。位移是球的最终位置和初始位置之间的差值。设运动球的最终位置和初始位置分别为 df 和 di。那么球的位移为

$$\mathrm{位移=d_f-d_i}$$

位移的单位也是米 (m)。它基于 SI 单位制。位移的量纲公式为 M⁰ L¹ T⁰。位移的例子包括老师在黑板前前后移动，以及有人在矩形路径上玩耍。

路径长度和距离有什么区别？

• 距离是物体在任意两点之间行进的长度。

• 物体的路径长度是物体在两点之间行进的距离。因此，路径长度和距离相同。两者的 SI 单位都是 m。

路径长度和位移的区别

路径长度	位移
物体到达目的地所经过的路径的总长度	在一定时间内按照运动方向行进的距离称为位移。
标量	矢量
它取决于路径	它不取决于路径
路径长度总是正的	位移可以为零或负

结论

如果物体正在改变其位置，则表示它处于运动状态。它可以是线性运动或圆周运动。需要三个坐标来描述物体在空间中的位置。物体位置的变化称为位移。物体初始位置和最终位置之间长度的大小为路径长度。

常见问题

1. 描述牛顿第一运动定律。

牛顿第一定律意味着粒子在不施加外力的情况下不会改变其运动或静止状态。例如，静止位置的盒子通过施加力来移动。如果不施加力，它就不能移动。同样，滚动球在不施加力的情况下也不能停止运动。

2. 为什么位移是矢量量而距离是标量？

距离的测量只考虑路径长度的大小，而位移的测量同时考虑大小和方向。

3. 距离或位移可以为负吗？

距离不能为负，因为它是一个标量。但位移可以为负，因为它也表示方向。因此，位移的负号表示方向。

4. 当力突然停止时，角运动会发生什么？

如果物体沿圆周路径运动，这主要是由于其上的向心力。这就是它在同一路径上旋转的原因。如果力停止，则物体将在切向方向上进行线性运动。

5. 区分矢量和标量。

标量	矢量
仅给出大小	给出方向和大小
仅用于一维问题	它用于多维问题
它可以分解成另一个标量	它不能分解成另一个矢量量
例如：距离、速度	例如：位移、速度