x = t 时刻的位置
x= t²- 2t
求前 1 秒和 2 秒内的距离和位移。

如给定，$x$ = $t$ 时刻的位置

$x=t^2-2t$

因此，速度 $v=\frac{dx}{dt}=2t-2$

让我们检查不同时间间隔的速度符号。

当 $t=0$ 时，$v=-2\ unit/s$

当 $t=1\ s$ 时，$v=2\times1-2=0\ unit/s$

当 $t=2\ s$ 时，$v=2\times2-2=2\ unit/s$

当 $t=0$ 时，$x=0$

当 $t=1\ s$ 时，$x=1^2-2\times 1=1-2=-1$

当 $t=2\ s$ 时，$x=2^2-2\times2=4-4=0$

因此，我们可以说在第一秒内，物体向负 x 轴移动了 1 个单位。并在前 2 秒内返回到正 x 轴，如图形所示。

因此，前 1 秒内的位移 = 位置变化 = 1 个单位

物体在前 1 秒内移动的距离 = 1 个单位

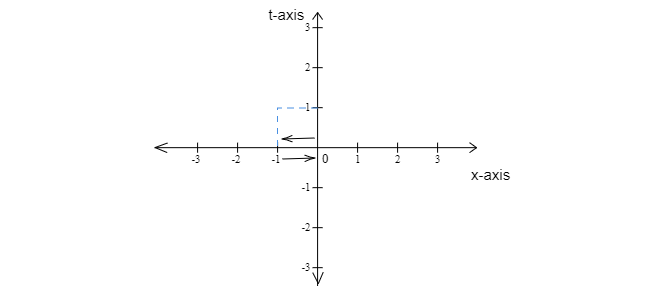
在前 2 秒内，$x=0$ 表示物体返回到 0，朝向正 x 轴。

因此，位移 = 0，因为物体返回到其初始位置。

在前 2 秒内，移动的距离 = 移动路径的总长度 = 1 个单位 + 1 个单位 = 2 个单位

教程点

更新于: 2022 年 10 月 10 日

32 次浏览

开启您的 职业生涯

完成课程获得认证

开始学习