在直角三角形PQR中，∠Q为直角，PQ = 4厘米，RQ = 3厘米。求sin P、sin R、sec P和sec R的值。

已知

在直角三角形PQR中，∠Q为直角，PQ = 4厘米，RQ = 3厘米。

要求

我们必须求sin P、sin R、sec P和sec R的值。

解:  


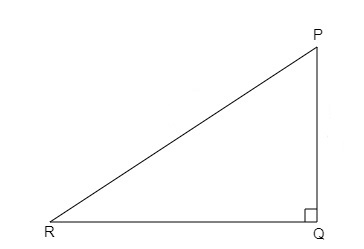
我们知道，

在以Q为直角的直角三角形PQR中，

根据勾股定理，

PR²=PQ²+QR²

根据三角函数的定义，

sin P=对边/斜边=QR/PR

sin R=对边/斜边=PQ/PR

sec P=斜边/邻边=PR/PQ

sec R=斜边/邻边=PR/QR

这里，PQ = 4厘米，RQ = 3厘米。

PR²=PQ²+QR²

⇒ PR²=(4)²+(3)²

⇒ PR²=16+9

⇒ PR=√25=5

因此，

sin P=QR/PR=3/5

sin R=PQ/PR=4/5

sec P=PR/PQ=5/4

sec R=PR/QR=5/3 

更新于: 2022年10月10日

94 次查看

开启你的职业生涯

完成课程获得认证

开始学习
广告