在直角三角形$ΔPQR$中，$\angle Q$为直角，$PR + QR = 25\ cm$，$PQ = 5\ cm$。求$sin\ P, cos\ P$和$tan\ P$的值。

已知

在直角三角形$ΔPQR$中，$\angle Q$为直角，$PR + QR = 25\ cm$，$PQ = 5\ cm$。

要求

我们需要求$sin\ P, cos\ P$和$tan\ P$的值。

解：  

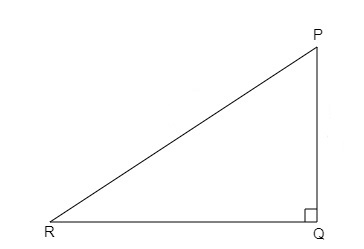
我们知道，

在以$Q$为直角的直角三角形$PQR$中，

根据勾股定理，

$PR^2=PQ^2+QR^2$

$\mathrm{PQ}^{2}=\mathrm{PR}^{2}-\mathrm{QR}^{2}$

$(5)^{2} =(\mathrm{PR}+\mathrm{QR})(\mathrm{PR}-\mathrm{QR})$

$25=25(\mathrm{PR}-\mathrm{QR})$

$\mathrm{PR}-\mathrm{QR}=1$

$\mathrm{PR}+\mathrm{QR}=25$

这意味着，

$\mathrm{PR}-\mathrm{QR}+\mathrm{PR}+\mathrm{QR}=1+25$

$=26$

$2PR=26$

$PR=13$

$\Rightarrow QR=PR-1$

$=13-1$

$=12$

根据三角函数比的定义，

$sin\ P=\frac{对边}{斜边}=\frac{QR}{PR}$

$=\frac{12}{13}$

$cos\ P=\frac{邻边}{斜边}=\frac{PQ}{PR}$

$=\frac{5}{13}$

$tan\ P=\frac{对边}{邻边}=\frac{QR}{PQ}$

$=\frac{12}{5}$

教程点

更新于: 2022年10月10日

45 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习