在直角三角形\( \Delta P Q R \)中，\( \angle Q \)为直角，\( P Q=3 \mathrm{~cm} \)且\( P R=6 \mathrm{~cm} \)。求\( \angle P \)和\( \angle R \)的度数。
已知
在\( \Delta P Q R \)中，\( \angle Q \)为直角，\( P Q=3 \mathrm{~cm} \)且\( P R=6 \mathrm{~cm} \)。
要求
我们必须确定\( \angle P \)和\( \angle R \)的度数。
解:
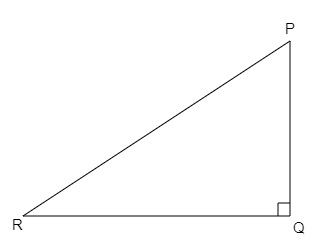
在\( \Delta P Q R \)中，
\( \sin R=\frac{PQ}{PR} \)
\( =\frac{3}{6} \)
\( =\frac{1}{2} \)
\( =\sin 30^{\circ} \) (\( \sin 30^{\circ}=\frac{1}{2} \))
\( \Rightarrow R=30^{\circ} \)
我们知道三角形的内角和为\( 180^o \)。
因此，
\( \angle P+\angle Q+\angle R=180^o \)
\( \angle P+90^o+30^o=180^o \)
\( \angle P=180^o-120^o \)
\( \angle P=60^o \)
因此，\( \angle P=60^o \)且\( \angle R=30^o \)。
- 相关文章
- 如图所示，\( O Q: P Q=3: 4 \)且\( \Delta P O Q \)的周长为\( 60 \mathrm{~cm} \)。求\( P Q, Q R \)和\( O P \)的长度。
- 画一个三角形\( P Q R \)，其中\( Q R=7 \mathrm{~cm} \)，\( P Q=6 \mathrm{~cm} \)且\( \angle P Q R=60^{\circ} \)。然后画另一个三角形，其边长分别是\( \triangle P Q R \)对应边长的\( 3 / 5 \)。
- 在下图中，\( \mathrm{PQR} \)是一个以\( \mathrm{Q} \)为直角的直角三角形，且\( \mathrm{QS} \perp \mathrm{PR} \)。如果\( P Q=6 \mathrm{~cm} \)且\( P S=4 \mathrm{~cm} \)，求\( Q S, R S \)和\( Q R \)的长度。
- 在下图中，\( PR=SQ \)且\( SR=PQ \)。a) 证明\( \angle P=\angle S \)。b) \( \Delta SOQ \cong \Delta POR \)
- 在三角形\( P Q R \)中，\( N \)是\( PR \)上的一点，使得\( Q N \perp P R \)。如果\( PN \cdot NR=QN^2 \)，证明\( \angle PQR=90^{\circ} \)。
- 画一个三角形\( P Q R \)使其外接圆半径为\( 8 \mathrm{~cm} \)，使得\( Q R \)被切点\( T \)分成\( Q T \)和\( TR \)两段，长度分别为\( 14 \mathrm{~cm} \)和\( 16 \mathrm{~cm} \)。如果\( \Delta P Q R \)的面积为\( 336 \mathrm{~cm}^{2} \)，求\( PQ \)和\( PR \)的长度。
- 如果\( p,\ q,\ r \)成等差数列，则证明\( p^2( p+r),\ q^2( r+p),\ r^2( p+q) \)也成等差数列。
- 化简下列式子：a) \( (l^{2}-m^{2})(2 l+m)-m^{3} \) b) \( (p+q+r)(p-q+r)+pq-qr \)
- 在\(\triangle PQR\)中，如果\(PQ=10\ cm\)，\(QR=8\ cm\)且\(PR=6\ cm\)，则求\(\angle R=?\)
- 在\(\triangle PQR\)中，\(\angle Q\)为直角，\(PQ = 4\ cm\)且\(RQ = 3\ cm\)。求\( \sin P, \sin R, \sec P \)和\( \sec R \)的值。
- 如果\( p=-2,\ q=-1 \)且\( r=3 \)，求\( p-q-r \)的值。
- 如果p, q和r成比例，且q = 17，r = 289，求p。
- 在下图中，\( \mathrm{PA}, \mathrm{QB}, \mathrm{RC} \)和\( \mathrm{SD} \)都垂直于直线\( l \)，\( \mathrm{AB}=6 \mathrm{~cm} \)，\( \mathrm{BC}=9 \mathrm{~cm} \)，\( CD=12 \mathrm{~cm} \)且\( SP=36 \mathrm{~cm} \)。求\( PQ, QR \)和\( RS \)的长度。
- \( A \)和\( B \)分别是三角形\( PQR \)的边\( PQ \)和\( PR \)上的点，使得\( \mathrm{PQ}=12.5 \mathrm{~cm} \)，\( \mathrm{PA}=5 \mathrm{~cm} \)，\( \mathrm{BR}=6 \mathrm{~cm} \)且\( \mathrm{PB}=4 \mathrm{~cm} \)。\( \mathrm{AB} \| \mathrm{QR} \)吗？请说明理由。
- 如图所示，从外点\( P \)引圆的切线\( PQ \)和\( PR \)，圆心为\( O \)，使得\( \angle RPQ=30^{\circ} \)。画一条弦\( RS \)平行于切线\( PQ \)。求\( \angle RQS \)的度数。
数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究