数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究用 C++ 表示的杜德尼数
给定基数中的数学数字在数论中定义为等于另一个自然数的完全立方的一个自然数，且第一个自然数的位数和等于第二个数字的位数和(维基百科)。
该数字由亨利·杜德尼发现。其数学公式如下 −
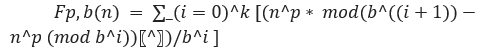
这里，给定一个整数 n。我们的任务是检查给定的数字 n 是否是杜德尼数 。
我们举个例子来理解一下问题，
输入： N = 17592
输出： 否
解释：
给定的数字不是杜德尼数。
解决方案方法 −
解决方案在于杜德尼数的基本定义。一个数字是杜德尼数基于数字的立方根等于其位数和。
算法 −
步骤 1： 检查 n 是否是一个完全立方。
步骤 2.1： 如果为“是”，则检查 n 的立方根 = n 的位数和。
步骤 2.2.1： 如果为“是”，则该数字是杜德尼数 。
步骤 2.2.2： 如果为“否”，则该数字不是杜德尼 数 。
步骤 2.2： 如果为“否”，则该数字不是杜德尼数。
展示我们的算法的工作原理的 C++ 程序 −
示例
#include <bits/stdc++.h>
using namespace std;
int calcDigitSum(int n){
int digitSum = 0;
int digitVal;
while (n > 0) {
digitVal = n % 10;
digitSum += digitVal;
n /= 10;
}
return digitSum;
}
int checkDudeney(int N) {
int cubeRoot = int( round( cbrt(N) ) );
if(pow(cubeRoot, 3.0) != N){
return 0;
}
int sumOfDigit = calcDigitSum(N);
if (cubeRoot != sumOfDigit)
return 0;
return 1;
}
int main() {
int N = 104323;
cout<<"The number "<<N;
if (checkDudeney(N))
cout<<" is a dudeney number.";
else
cout<<" is not a dudeney number.";
return 0;
}输出 −
The number 104323 is not a dudeney number.
更新于： 2021-01-22
512 次浏览
广告