解释波的振幅。画出波的示意图，并在图上标出它的振幅。

---

介绍

波是一种从一点传播到另一点的连续扰动。有不同类型的波通过介质传播。主要有两种类型的波。

机械波：需要介质才能传播的波。例如，声信号在介质中传播，水波在水中传播。

电磁波：这些波在真空中传播。例如，光波在太空中传播。

通常，波以波峰和波谷的形式传播，每个波都有一些特性，例如振幅、速度、频率等等。在描述波时，振幅是能量的度量。对于电磁辐射，波是穿过介质或穿过空的空间的能量脉冲。

定义波的振幅

振幅是波传递能量的度量；投入波中的能量越多，振幅就越大，或者峰值或谷值到轴线的距离就越大，这被称为波的振幅 (A)。

振幅以米 (m) 为单位表示。波的振幅决定了它携带多少能量。它估计波的起伏程度。如果波的振幅大，则能量高，而振幅小的波能量低。正弦波的方程可以写成

$$\mathrm{x=A\:sin(\omega t+\Phi)}$$

其中：x=波的位移

A=波的振幅

ω=角频率

t=时间

ϕ=相位角

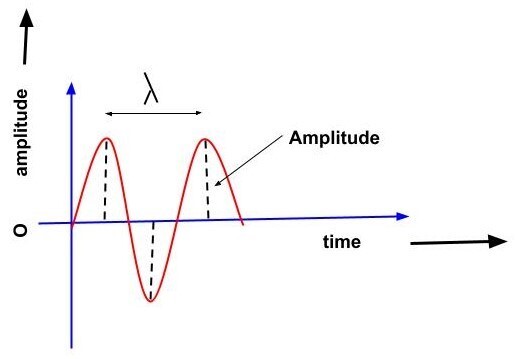
产生粒子运动所需的能量以位移的程度表示，这被估计为波的振幅。

声音

声音是一种引起物体振动的能量。这些振动通过固体、液体或气体等介质将能量从一个地方传递到另一个地方。由于声音是一种纵波，因此它以压缩和稀疏的形式传播。当一个物体发出声音时，物体的振动将其能量传递给空气分子，引起连锁反应，该反应通过空气传播，直到到达我们的耳膜。当我们的耳朵拾取到声音时，信号就会传递到我们的大脑，让我们理解我们听到的内容。

人类可以听到的声音频率范围为 20Hz 至 20KHz，高于和低于此范围的声音被称为超声波和次声波。超声波：这些波主要用于医学领域，用于诊断各种疾病，如心电图、超声波检查、体外碎石术等等。

次声波：它是一种低频波，最常见于火山爆发、地震等自然现象中。

在物理学中定义振幅？

振幅是由振动体或波上的一点与其静止点之间的最大距离或位移决定的。所有波都携带一定的振幅。

在物理学中，波的振幅可以通过调幅来调制。在这个过程中，低振幅波在载波的帮助下将数据从源传输到目的地。这种调幅应用于信号传输、广播等。

声音的特性

音调

声音的音调是频率的感觉。高频声波指的是高音调的声音，而低频声波则与低音调的声音相关。它以赫兹 (Hz) 为单位表示。

响度

波的大小决定了声音的响度现象。如果声波的大小很大，则表示信号响亮。它以分贝 (dB) 为单位表示。

振幅

它是声波穿过介质时扰动的粒子的最大位移。它以米 (m) 为单位表示。

波长

声音是一种纵波，它通过介质传播并经历压缩和稀疏。它是两个连续的稀疏或压缩的核心之间的空间，或者压缩长度加上相邻稀疏的长度。它以埃 (Å) 为单位表示，等于 10^-10 米。

$$\mathrm{\lambda=\frac{
u}{f}}$$

频率

每秒产生的声波数量称为频率。如果一个波的频率低，则它的波比高频波少。声音的频率以赫兹 (Hz) 估计。

$$\mathrm{f=\frac{1}{T}}$$

周期

介质粒子完成一次振动所需的时间称为波的周期。它以秒(秒) 为单位表示。

$$\mathrm{T=\frac{1}{f}}$$

速度

声波的速度是扰动从一个粒子传播到下一个粒子的速率。它以 (ms^-1) 为单位表示。

$$\mathrm{速度=位移/时间}$$

结论

在我们的日常生活中，我们会遇到各种各样的波，例如太阳波、水波和声波。波只是能量以扰动形式的传递。

声波是由振动物体产生的，它将能量传递给大气中存在的分子。因此，声波得以传播。声音有很多种，例如悦耳的声音、噪音、音乐等等。声音的特性在音乐或任何其他类型的声音的产生中起着重要的作用。

常见问题

Q1. 写出音调和响度之间的区别？

答：

音调	响度
声音的音调是频率的感觉。高频声波指的是高音调的声音，而低频声波则与低音调的声音相关。	声波的振幅决定了声音的响度现象。如果声波的振幅大，则声音响亮。
音调的SI单位是赫兹(Hz)。	响度的SI单位是分贝 (dB)。
音调与频率成正比。	响度与振幅的平方成正比。

表1：音调和响度之间的区别

Q2. 区分音调和频率？

答：频率指的是事件发生的频率。为简单起见，我们将频率定义为每秒发生的次数。音调是一个与频率密切相关的术语。声音振荡的频率与其音调成正比。频率的特性在所有类型的波中都有体现，包括电磁波和机械波。音调是一个专门针对声波的特性。音调是一个难以定义的概念。

Q3. 人耳的听力范围是多少？

答：人可以感知20 Hz至20 kHz频率范围内的声波。(有趣的是，新生儿可以听到略高于20 kHz的频率，但随着年龄的增长，他们会失去一些高频灵敏度。)

Q4. 写出显示波长、频率和速度之间相关性的方程式？

答：波长、频率和速度之间的关系可以用以下方程式表示。

$$\mathrm{\lambda=
u/f}$$

正如我们在公式中看到的；波长和速度成正比，而波长和频率成反比。速度和频率成正比。

Q5. 写出三种不同格式的波长方程式。

答：求波长

$$\mathrm{λ=
u/f}$$

求频率

$$\mathrm{f=
u/\lambda}$$

求速度

$$\mathrm{
u=f×\lambda}$$