图示为一个振荡的单摆。

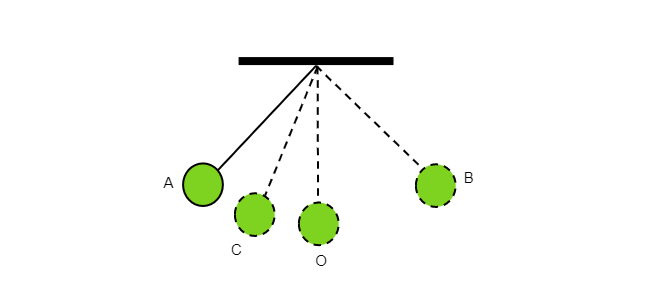
摆球从A点运动到C点所用的时间为$t_1$

从A到C的时间 $=t_{AC}=t_1$

从C到O的时间 $=t_{CO}=t_2$

因此，从A到O的时间 $=t_{AO}=t_1+t_2$

类似地，从O到B的时间 $=t_{OB}=t_1+t_2$

从A到B的总时间 $=t_{AB}=t_{AO}+t_{OB}=t_1+t_2+t_1+t_2$

$=2(t_1+t_2)$

类似地，从B到A的时间 $=2(t_1+t_2)$

我们知道，周期是从A到B再从B到A所用的时间。

因此，简单摆的周期 $T=t{AB}+t_{BA}=2(t_1+t_2)+2(t_1+t_2)$

$=4(t_1+t_2)$

因此，选项$(d)$是正确的。

教程点

更新于: 2022年10月10日

93 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习