Python 中填充书架

假设我们有一系列书籍 - 这里第 i 本书的厚度为 books[i][0]，高度为 books[i][1]。如果我们想按顺序将这些书放在总宽度为 shelf_width 的书架上。如果我们选择一些书放在这个书架上（使得它们的厚度之和 <= shelf_width），然后构建书柜的另一层，书柜的总高度增加了我们可以放下的书籍的最大高度。我们将重复此过程，直到没有更多书籍可以放置。我们必须记住，在上述过程的每个步骤中，我们放置书籍的顺序与给定的书籍序列的顺序相同。我们必须找到以这种方式放置书架后书架的总高度的最小可能高度。因此，如果输入类似于 - [[1,1], [2,3], [2,3], [1,1], [1,1], [1,1], [1,2]]，并且 self_width = 4，

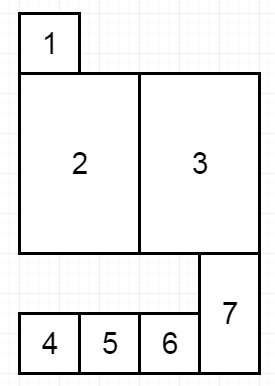
则输出将为 6，因为 3 个书架的高度之和为 1 + 3 + 2 = 6。请注意，第 2 本书不必放在第一个书架上。

为了解决这个问题，我们将遵循以下步骤 -

  • 创建一个大小与 books 相同的数组 dp，并使用无限填充它
  • dp[0] := books[0,1]
  • 对于 i 从 1 到 books 的长度 - 1
    • curr_height := 0
    • temp := self_width
    • j := i
    • 当 j >= 0 且 temp – books[j, 0] >= 0 时，执行
      • curr_height := books[j, 1] 和 curr_height 的最大值
      • dp[i] := dp[i]、curr_height + (如果 j – 1 >= 0 则为 dp[j - 1]，否则为 0) 的最小值
      • temp := temp – books[j, 0]
      • 将 j 减 1
  • 返回 dp 的最后一个元素

让我们看看以下实现以更好地理解 -

示例

class Solution(object):
   def minHeightShelves(self, books, shelf_width):
      """
      :type books: List[List[int]]
      :type shelf_width: int
      :rtype: int
      """
      dp = [float('inf') for i in range(len(books))]
      dp[0] = books[0][1]
      for i in range(1,len(books)):
         current_height = 0
         temp = shelf_width
         j = i
         while j>=0 and temp-books[j][0]>=0:
            current_height = max(books[j][1],current_height)
            dp[i] = min(dp[i],current_height +( dp[j-1] if j-1 >=0 else 0))
            temp-=books[j][0]
            j-=1
         #print(dp)
      return dp[-1]

输入

[[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]]
4

输出

6

更新于: 2020-03-05

474 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习
广告