数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在 Java 中查找平衡 BST 中具有给定和的配对
概念
针对给定的平衡二叉搜索树和目标和，我们编写一个函数，如果存在和等于目标和的配对，则返回 true，否则返回 false。在这种情况下，期望的时间复杂度为 O(n)，并且只能实现 O(Logn) 的额外空间。在此，不允许对二叉搜索树进行任何修改。我们需要注意的是，平衡 BST 的高度始终为 O(Logn)。
示例
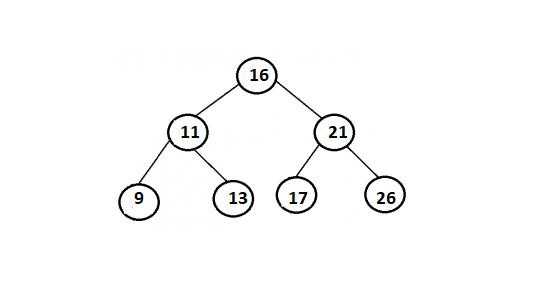
方法
根据蛮力解决方案，我们考虑 BST 中的每一对，并验证其和是否等于 X。此解决方案的时间复杂度将为 O(n^2)。
现在，一个更好的解决方案是构建一个辅助数组，并将 BST 的中序遍历存储在数组中。在这种情况下，数组将被排序，因为 BST 的中序遍历始终生成排序数据。因此，在中序遍历可用后，我们可以在 O(n) 时间内配对。请记住，此解决方案在 O(n) 时间内工作，但需要 O(n) 的辅助空间。
示例
// Java code to find a pair with given sum
// in a Balanced BST
import java.util.ArrayList;
// A binary tree node
class Node1 {
int data1;
Node1 left1, right1;
Node1(int d){
data1 = d;
left1 = right1 = null;
}
}
public class BinarySearchTree {
// Indicates root of BST
Node1 root1;
// Indicates constructor
BinarySearchTree(){
root1 = null;
}
// Indicates inorder traversal of the tree
void inorder(){
inorderUtil1(this.root1);
}
// Indicates utility function for inorder traversal of the tree
void inorderUtil1(Node1 node1){
if (node1 == null)
return;
inorderUtil1(node1.left1);
System.out.print(node1.data1 + " ");
inorderUtil1(node1.right1);
}
// Now this method mainly calls insertRec()
void insert(int key1){
root1 = insertRec1(root1, key1);
}
/* Indicates a recursive function to insert a new key in BST */
Node1 insertRec1(Node1 root1, int data1){
/* So if the tree is empty, return a new node */
if (root1 == null) {
root1 = new Node1(data1);
return root1;
}
/* Otherwise, recur down the tree */
if (data1 < root1.data1)
root1.left1 = insertRec1(root1.left1, data1);
else if (data1 > root1.data1)
root1.right1 = insertRec1(root1.right1, data1);
return root1;
}
// Indicates method that adds values of given BST into ArrayList
// and hence returns the ArrayList
ArrayList<Integer> treeToList(Node1 node1, ArrayList<Integer> list1){
// Indicates Base Case
if (node1 == null)
return list1;
treeToList(node1.left1, list1);
list1.add(node1.data1);
treeToList(node1.right1, list1);
return list1;
}
// Indicates method that checks if there is a pair present
boolean isPairPresent(Node1 node1, int target1){
// Now this list a1 is passed as an argument
// in treeToList method
// which is later on filled by the values of BST
ArrayList<Integer> a1 = new ArrayList<>();
// Now a2 list contains all the values of BST
// returned by treeToList method
ArrayList<Integer> a2 = treeToList(node1, a1);
int start1 = 0; // Indicates starting index of a2
int end1 = a2.size() - 1; // Indicates ending index of a2
while (start1 < end1) {
if (a2.get(start1) + a2.get(end1) == target1) // Target Found!{
System.out.println("Pair Found: " + a2.get(start1) + " + " + a2.get(end1) + " " + "= " + target1);
return true;
}
if (a2.get(start1) + a2.get(end1) > target1)
// decrements end
{
end1--;
}
if (a2.get(start1) + a2.get(end1) < target1)
// increments start
{
start1++;
}
}
System.out.println("No such values are found!");
return false;
}
// Driver function
public static void main(String[] args){
BinarySearchTree tree1 = new BinarySearchTree();
/*
16
/ \
11 21
/ \ / \
9 13 17 26 */
tree1.insert(16);
tree1.insert(11);
tree1.insert(21);
tree1.insert(9);
tree1.insert(13);
tree1.insert(17);
tree1.insert(26);
tree1.isPairPresent(tree1.root1, 34);
}
}输出
Pair Found: 13 + 21 = 34
更新于： 2020-07-23
162 次查看
广告