基尔霍夫定律的推广

---

简介

基尔霍夫定律用于研究电路中使用的电能。带电粒子的运动是电能的来源。从带电粒子的动能或势能获得的能量就是电能。带电粒子是指带电的原子、分子或离子。

带电粒子之间存在吸引力或排斥力，这取决于库仑定律。电流通过称为电路的闭合路径从一点流向另一点。电流通过这条闭合路径。我们使用许多电子元件，例如晶体管、电阻、电容器等。许多电子设备，如计算机、DVD 播放器等，都是由这些电子元件组成的。

以图形方式表示的电路称为电路图。电路图的主要应用是设计、构建和维护电气和电子电路。

什么是基尔霍夫定律？

古斯塔夫·罗伯特·基尔霍夫是一位德国物理学家，他发展了电路定律。他在许多物理学领域进行了研究，例如电路、光谱学和黑体辐射。

基尔霍夫第一定律

基尔霍夫第一定律是关于流过电路的电流。它也称为基尔霍夫电流定律（KCL）。根据该定律，在节点处，进入节点的电流总量等于离开节点的电流总量，前提是在节点处没有电荷损失。也可以表述为流入和流出电路的电流之和等于零。它基于电荷守恒定律的原理。因此，根据基尔霍夫第一定律，

$$\mathrm{流入电路的电流总和=流出电路的电流总和}$$

让我们在以下电路中应用基尔霍夫第一定律，然后得到：

$$\mathrm{i_1+i_3+i_4=i_2+i_5}$$

通过将流入电路的电流视为正，流出电路的电流视为负，它也可以用另一种形式表示，例如

$$\mathrm{i_1-i_2+i_3+i_4-i_5=0}$$

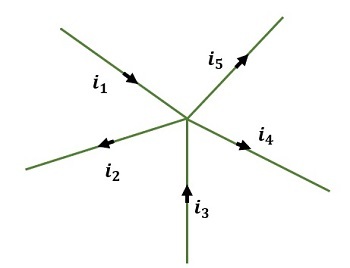
图 1：节点定律

基尔霍夫定律适用于分布式网络。它不依赖于网络的性质，例如有源、无源、线性或非线性。电流始终流过电阻较低的路径。

基尔霍夫第二定律

基尔霍夫第二定律规定了电路上的电压降。它也称为基尔霍夫电压定律。它是电荷守恒和能量守恒的结果。沿电路闭合回路特定方向的电压之和为零。根据欧姆定律，元件上的电压为 $\mathrm{V=IR}$

让我们在以下闭合回路中应用基尔霍夫第二定律，然后得到：

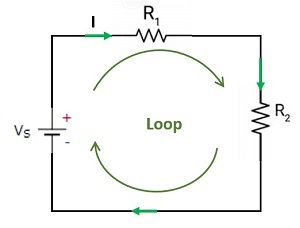
图 2：电压定律

$$\mathrm{V_s=IR_1+IR_2}$$

KVL 用于所有电路，无论电路的性质如何。它用于电荷守恒和能量守恒原理。在并联路径中，电压是恒定的，而在串联路径中，电压是分开的。

定律的推广

基于观察或实验在任何两种现象之间建立一般性真理的过程称为定律的推广。通过进行多次实验来推广定律。

用途

基尔霍夫定律在许多领域都有应用。如果电流通过电路，则在不同的电路区域会产生电压降。基尔霍夫定律用于查找流过电路的电流量以及电路上的电压降。它给出了流过电路的电流方向。

优点

基尔霍夫定律描述了包含许多元件的电路中电流的分布。它提供了一种在复杂的直流电路中找到电压的方法。根据该定律，可以找到电路的内阻。基尔霍夫第一定律的最佳应用之一是惠斯通电桥。

应用

基尔霍夫定律的应用之一是惠斯通电桥，用于查找未知电阻。它使用了两个定律。让我们考虑四个电阻 P、Q、R 和 S，它们以闭合回路连接，电池和检流计以以下方式连接。设通过电阻 P、Q、R 和 S 的电流分别为 $\mathrm{i_1,i_3,i_2}$ 和 $\mathrm{i_4}$。通过检流计的电流为 ig。此处，基尔霍夫定律应用于节点 C 和 F。

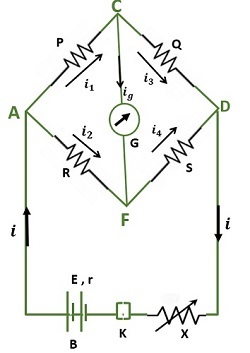
图 3：惠斯通电桥

在节点 C 应用该定律，我们得到：

$$\mathrm{i_1-i_3-i_g=0}$$

$$\mathrm{i_1=i_3+i_g………………………………(1)}$$

在节点 F，我们得到：

$$\mathrm{i_2+i_g-i_4=0}$$

$$\mathrm{i_4=i_2+i_g………………………………..(2)}$$

在平衡条件下，ig = 0。然后 (1) 和 (2) 将变为

$$\mathrm{i_1=i_3}$$

$$\mathrm{i_4=i_2}$$

因此，基尔霍夫第一定律应用于惠斯通电桥的一部分。

在回路ACFA 和CDFC 中应用第二定律，我们得到：

$$\mathrm{i_1 P+i_g G-i_2 R=0……………………………(3)}$$

$$\mathrm{i_3 Q-i_4 S-i_g G=0 ………………………(4)}$$

在平衡条件下，ig = 0。然后 (3) 和 (4) 将变为

$$\mathrm{i_1 P\:-\:i_2 R\:=\:0}$$

$$\mathrm{i_1 P=i_2 R………………………..(5)}$$

$$\mathrm{i_3 Q-i_4 S=0}$$

$$\mathrm{i_3 Q=i_4 S……………………………..(6)}$$

将方程 (5) 除以 (6)

$$\mathrm{\frac{i_1 P}{i_3 Q}=\frac{i_2 R}{i_4 S}}$$

此处 $\mathrm{i_1=i_3}$ 和 $\mathrm{i_4=i_2}$ 因此

$$\mathrm{\frac{i_1 P}{i_1 Q}=\frac{i_2 R}{i_2 S}}$$

$$\mathrm{\frac{P}{Q}=\frac{R}{S}}$$

通过此公式，可以计算电路中的未知电阻。

局限性

由于磁场引起的感应电动势，基尔霍夫定律仅适用于高频交流电路。基尔霍夫电流定律适用于电路电流恒定的情况。如果假设闭合电路中的磁场不发生变化，则仅适用 KVL。它基于忽略电路中电场的条件。

结论

在本教程中，讨论了基尔霍夫定律和该定律的推广。还详细讨论了基尔霍夫定律的用途和局限性。

常见问题解答

Q1. 电路的特征是什么？

答：电路必须是闭合回路，因为它具有回流路径。每个电路都应该至少有一个电源。也就是说，它应该包含至少一个有源元件。电路包含串联或并联连接的有源和无源元件。在电路中，电子从负极流向正极。

Q2. 电荷守恒定律是什么？

答：它指出，如果电路是孤立的，则电路中的总电荷不会改变，并且保持恒定。换句话说，它也可以说明电荷既不能被创造也不能被消灭。

Q3. 能量守恒是什么？

答：根据能量守恒定律，一种形式的能量可以转化为另一种形式的能量，并且能量既不能被消灭也不能被创造。换句话说，它也可以说明，如果系统是孤立的，则系统的总能量不会改变，并且保持恒定。

Q4. 说明欧姆定律

答：它给出了电路中的电流与电路上的电压之间的关系。当所有物理条件（包括温度）恒定时，它给出了电流与电压之间的比例关系。欧姆定律方程为

$$\mathrm{V=IR}$$

R 是比例常数，它是电路对电流的电阻。

Q5. 欧姆定律的应用是什么？

答：它用于在直流电流表和直流分流器中分流电流。使用欧姆定律计算电路的电流、电压和电阻。使用欧姆定律维持所需的电压降。