数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究DEPQ 的通用方法
双堆
存在从单端优先队列 (PQ) 数据结构推导出高效 DEPQ（双端优先队列）数据结构的通用方法，这些方法也提供了 remove(aNode) 操作的高效实现（此操作从 PQ 中消除节点 aNode）。最简单的方法，即双结构方法，同时跟踪所有 DEPQ 元素的最小 PQ 和最大 PQ，并在最小 PQ 和最大 PQ 的节点之间保持对应指针，这些节点包含相同的元素。
图 A 显示了元素 7、8、3、6、5 的双堆结构。对应指针显示为红色箭头。
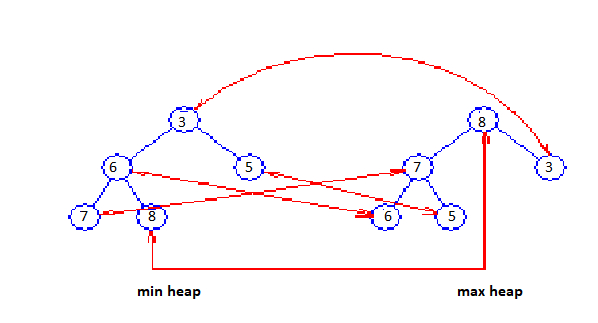
图 A：双堆
虽然图中显示每个元素都存储在最小堆和最大堆中，但实际上只需要在两个堆中的一个中存储每个元素。
isEmpty 和 size 操作是通过实现一个跟踪 DEPQ 中元素数量的变量 size 来实现的。最小元素位于最小堆的根部，最大元素位于最大堆的根部。要插入元素 A，我们将 A 插入到最小堆和最大堆中，然后在 A 在最小堆和最大堆中的位置之间设置对应指针。要消除最小元素，我们从最小堆中执行 removeMin，并从最大堆中执行 remove(aNode)，其中 aNode 是已移除元素的对应节点。最大元素的消除方式类似。
总对应和叶对应
总对应和叶对应是更复杂的对应技术。在这两种技术中，一半的元素位于最小 PQ 中，另一半位于最大 PQ 中。当元素数量为奇数时，一个元素存储在缓冲区中。此缓冲区元素不属于任何 PQ。在总对应技术中，最小 PQ 中的每个元素 x 都与最大 PQ 的不同元素 y 配对。(x, y) 是一个对应的元素对，使得 priority(x) <= priority(y)。
图 B 显示了 11 个元素 3、4、5、5、6、6、7、8、9、10、11 的总对应堆。元素 10 位于缓冲区中。对应对由红色箭头显示。
图 B：总对应堆
在叶对应技术中，最小和最大 PQ 的每个叶元素都需要成为对应对的一部分。非叶元素不需要在任何对应对中。图 C 显示了一个叶对应堆。
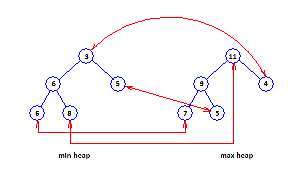
图 C：叶对应堆
总对应和叶对应结构比双结构需要更少的空间。但是，总对应和叶对应结构的 DEPQ 算法比双结构的算法更复杂。在三种对应技术中，叶对应是速度最快的 DEPQ 对应结构。
通过实现任何描述的对应技术，我们可以从堆、高度偏差左倾树和配对堆中得到 DEPQ 结构。在这些 DEQP 结构中，put(x)、removeMin() 和 removeMax() 操作消耗 O(log n) 时间（n 是 DEPQ 中的元素数量，对于配对堆，这是摊销复杂度），其余 DEPQ 操作消耗 O(1) 时间。
浏览量：112
