七边形数

---

七边形数是可以表示为七边形的数。七边形是一个有7条边的多边形。七边形数可以表示为七边形（7边多边形）的连续层组合。下图可以更好地解释七边形数。

第一个七边形数是1。因此，它可以用一个点来表示。

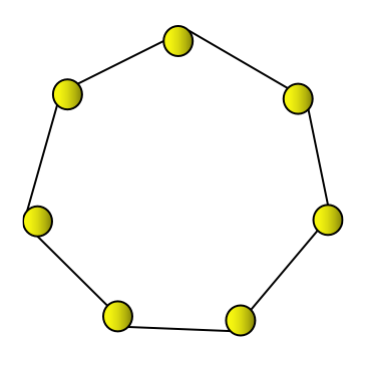
第二个七边形数是7，可以用一个七边形来表示。

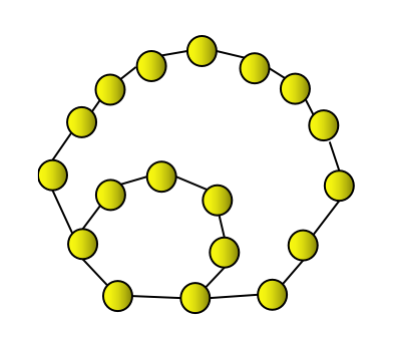
第三个七边形数是18，可以用一个七边形加上连续的一层七边形来表示。

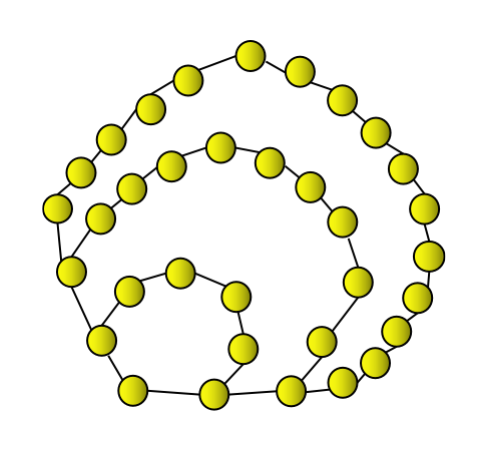
第四个七边形数是34。它可以用一个七边形加上上面所示的两个连续的七边形层来表示，结果为34。

后面的七边形数将使用类似的概念。按照同样的逻辑，前几个七边形数是1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403……

这个问题中的任务包括：我们将得到一个正数N作为输入，我们需要将第N个七边形数作为输出。

例如：

输入：N=6

输出 : 81

输入：N=9

输出 : 189

现在让我们来看看我们将用来解决这个问题的算法。

算法

为了解决这个问题，我们需要观察计算第n个七边形数所遵循的模式。第n个七边形数可以表示为：

$$Heptagonal_{n}\:=\:\frac{n}{2}(5n\:-\:3)$$

如果我们仔细观察表达式，每个七边形数的形式都是

$\frac{n}{2}(5n\:-\:3)$，其中n代表七边形数的个数。

让我们用例子来更好地理解它。

对于n=1，$\frac{1}{2}(5\:\times\:1\:-\:3)$= 1，这是第一个七边形数。

对于n=2，$\frac{2}{2}(5\:\times\:2\:-\:3)$= 7，这是第二个七边形数。

对于n=3，$\frac{3}{2}(5\:\times\:3\:-\:3)$= 18，这是第三个七边形数。

现在，让我们检查n=8。$\frac{8}{2}(5\:\times\:8\:-\:3)$得到148，这实际上是七边形数序列中的第八个七边形数。

由于我们可以使用上述表达式得到任何第n个七边形数，因此我们将在我们的方法中使用这个表达式来计算第n个七边形数，其中n可以是任何正数。

方法

我们将遵循的方法的逐步说明：

• 将任何正数N作为输入，以计算对应于值N的七边形数。

• 初始化一个函数来计算第N个七边形数。

• 使用算法部分中提到的表达式，即$\frac{N}{2}(5N\:-\:3)$来计算第N个七边形数，并将其存储在任何变量中。

• 返回我们存储值的变量，该值将是对应于任何正值N的第N个七边形数。

注意 - 我们将使用浮点型数据类型而不是整型数据类型，以避免在使用上述公式计算第N个七边形数时由于小数值而导致的任何错误。

示例

C++中方法的实现：

#include <bits/stdc++.h>
#include <iostream>
using namespace std;

//function to calculate nth heptagonal number using formula n/2(5n-3)
float heptagonal(float N){
   float ans= (N/2)*((5*N) - 3); //to store nth heptagonal number
   return ans;
}
int main(){
   float N=5; //input
   float a=heptagonal(N); //store the answer in a variable
   N=13;
   float b=heptagonal(N);
   cout<<a<<endl<<b<<endl; //print the answer
   return 0;
}

输出

55
403

时间复杂度：O(1)，因为花费常数时间。

空间复杂度：O(1)，因为没有占用额外的空间。

结论

我们尝试学习七边形数的概念以及用于计算第n个七边形数的公式，我们在方法中使用了该公式。

我希望您会发现这篇文章有助于学习为任何用户输入n打印第n个七边形数的概念。