十六进制数系统
十六进制数系统是一种数的表示方法,其基数为16。这意味着只有16个符号或可能的数字值,它们是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。其中A、B、C、D、E和F分别表示十进制值10、11、12、13、14和15。表示任何一位数字只需要4位。十六进制数通常用0x前缀或h后缀表示。
每一位数字都有一个权重,它是16的幂。十六进制系统中每个位置的有效数字都比前一位高16倍,这意味着十六进制数的数值是通过将数字的每一位乘以该位出现的位数的值,然后将乘积相加来确定的。因此,它也是一个位置(或加权)数系统。
十六进制数的表示
每个十六进制数都可以用4位表示,每组位的值在0000(对于0)和1111(对于F = 15 = 8+4+2+1)之间。十六进制数的等效二进制数如下所示。
| 十六进制数字 | 1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 |
| 二进制 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 十六进制数字 | 8 | 9 | A = 10 | B = 11 | C = 12 | D = 13 | E = 14 | F = 15 |
| 二进制 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
十六进制数系统类似于八进制数系统。十六进制数系统提供了一种方便的方法,可以将大的二进制数转换为更紧凑的小组。
| 最高有效位 (MSB) | 十六进制小数点 | 最低有效位 (LSB) | |||
|---|---|---|---|---|---|
| 162 | 161 | 160 | 16-1 | 16-2 | 16-3 |
| 256 | 16 | 1 | 1/16 | 1/256 | 1/4096 |
由于十六进制数系统的基数为16,因此数字的最大值为15,不能超过15。在这个数系统中,十六进制小数点左边的连续位置的权重分别为160、161、162、163等等。类似地,十六进制小数点右边的连续位置的权重分别为16-1、16-2、16-3等等。这称为16的幂次方。任何十六进制数的十进制值都可以通过将每个数字与其位置值相乘的乘积之和来确定。
示例-1 - 数字512解释为
512=2x162+0x161+0x160=200
这里,最右边的位0是最低有效位(LSB),最左边的位2是最高有效位(MSB)。
示例-2 - 数字2015.0625解释为
2015.0625=7x162+13x161+15x160+1x16-1=7DF.10
这里,最右边的位0是最低有效位(LSB),最左边的位7是最高有效位(MSB)。
示例-3 将十进制数21转换为十六进制表示
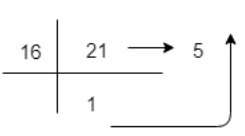
(21)10=1x161+5x160=(15)16 So, decimal value 21 is equivalent to 15 in Hexadecimal Number System.
十六进制数系统的应用
十六进制数系统通常用于计算机编程和微处理器。它还有助于描述网页上的颜色。三种原色(即红色、绿色和蓝色)中的每一种都由两位十六进制数字表示,以创建255个可能的值,从而产生超过1600万种可能的颜色。十六进制数系统用于描述每个字节的内存位置。对于计算机专业人员来说,这些十六进制数也比二进制数或十进制数更容易阅读和编写。
优点和缺点
使用十六进制数的主要优点是它使用更少的内存来存储更多数字,例如,它用两位数字存储256个数字,而十进制数用两位数字存储100个数字。此数系统也用于表示计算机内存地址。它只使用4位来表示二进制中的任何数字,并且易于在十六进制和二进制之间进行转换。以十六进制形式处理输入和输出更容易。在数据科学、人工智能和机器学习领域,它有很多优点。
十六进制数系统的主要缺点是人们可能不容易阅读和书写,而且难以使用十六进制数系统进行乘法、除法等运算。十六进制数是处理计算机数据最困难的数系统。
十六进制(16进制)数的15的补码和16的补码
简单来说,十六进制数的15的补码是从F(=15)中减去其每一位数字。例如,十六进制数2030的15的补码是FFFF - 2030 = DFCF。
十六进制数的16的补码是给定数字的15的补码加上最低有效位(LSB)的1。例如,十六进制数2020的16的补码是(FFFF - 2030) + 1 = DFDF + 1 = DFE0。请注意,十六进制数系统的最大数字是F(=15),因此F+1的加法将为0,进位为1。


 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP