二进制数系统
二进制数系统是一种数表示技术。它是数字系统中最流行和最常用的系统。二进制系统用于表示二进制量,这些量可以用任何只有两种工作状态或可能条件的设备来表示。例如,开关只有两种状态:开或关。
在二进制系统中,只有两个符号或可能的数字值,即0和1。由任何只有2个工作状态或可能条件的设备表示。二进制数通常通过添加0b前缀或2后缀来表示。
每位数字都有一个权重,它是2的幂。二进制系统中的每个位置都比前一个位置重要2倍,这意味着二进制数的数值是通过将数字的每一位乘以该位出现的位置的值,然后将乘积相加来确定的。因此,它也是一种位置(或加权)数系统。
| 最高有效位 (MSB) | 二进制小数点 | 最低有效位 (LSB) | |||
|---|---|---|---|---|---|
| 22 | 21 | 20 | 2-1 | 2-2 | 2-3 |
| 4 | 2 | 1 | 0.5 | 0.25 | 0.125 |
0V到0.8V之间的电压范围用于二进制逻辑0,2V到5V之间的电压范围用于二进制逻辑1。0.8V到2V之间的电压范围不用于,因为它可能会导致数字电路出错。
示例1 - 数字125解释为
125 = 1x26+1x25+1x24+1x23+1x22+0x21+1x20=1111101
这里,最右边的位1是最低有效位(LSB),最左边的位1是最高有效位(MSB)。
示例2 - 数字90.75解释为
90.75 = 1x26+0x25+1x24+1x23+0x22+1x21+0x20+1x2-1+1x2-2=1011010.11
这里,最右边的位1是最低有效位(LSB),最左边的位1是最高有效位(MSB)。
示例3 - 将十进制数21转换为二进制表示
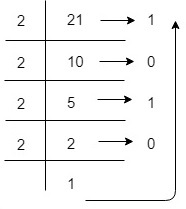
(21)10 =16+0+4+0+1 = 1x24+0x23+1x22+0x21+1x20 =(10101)2 So, decimal value 21 is equivalent to 10101 in Binary Number System.
二进制数系统的应用
二进制数系统在计算机技术中非常有用,计算机编程语言也使用二进制数系统,这有助于数字编码。二进制数系统也可以用于布尔代数。
优点和缺点
使用二进制的主要优点是它是一个易于电子设备表示的基数。二进制数系统在编码中也易于使用,计算更少,计算错误更少。
二进制数的主要缺点是对于人类来说难以阅读和编写,因为等效十进制数的二进制数位数很多。
二进制(2进制)数的1的补码和2的补码
要获得二进制数的1的补码,只需反转给定的数字。例如,二进制数110010的1的补码是001101。
二进制数的2的补码是给定数字的1的补码加上1到最低有效位(LSB)。例如,二进制数10010的2的补码是(01101) + 1 = 01110。


 数据结构
数据结构 网络
网络 关系数据库管理系统(RDBMS)
关系数据库管理系统(RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP